题目内容
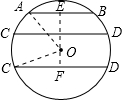
已知⊙O的半径为5cm,AB和CD是⊙O的弦,AB∥CD,AB=6cm,CD=8cm,求AB与CD之间的距离是多少?
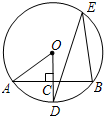
如图,作OE⊥AB于E,OF⊥CD于F,
则AE=
AB=3cm,CF=
CD=4cm,
∴OE=
=
=4,
OF=
=
=3,
(1)当AB、CD在圆心O的同侧时,距离为OE-OF=4-3=1(cm)(3分)
(2)当AB、CD在圆心O的异侧时,距离为OE+OF=4+3=7(cm)(6分)
因此,AB与CD之间的距离是1或7cm.
则AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴OE=
| OA2-AE2 |
| 52-32 |
OF=
| OC2-CF2 |
| 52-42 |
(1)当AB、CD在圆心O的同侧时,距离为OE-OF=4-3=1(cm)(3分)
(2)当AB、CD在圆心O的异侧时,距离为OE+OF=4+3=7(cm)(6分)
因此,AB与CD之间的距离是1或7cm.


练习册系列答案
相关题目