Question

如图所示，⊙O在△ABC三边截得的弦长相等，∠A=70°，求∠BOC．

Answer 1

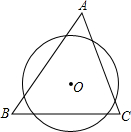
过O作OM⊥AB，ON⊥AC，OP⊥BC，垂足分别为M，N，P，
∵DE=FG=HI
∴OM=OP=ON
∴O是∠B，∠C平分线的交点
∵∠A=70°，
∴∠B+∠C=180°-∠A=110°，
又∵O是∠B，∠C平分线的交点，
∴∠BOC=180°-

1

2

（∠B+∠C）=180°-

1

2

×110°=125°．