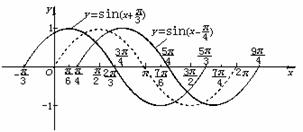
例 画出函数
y=sin(x+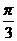 ),x∈R
),x∈R
y=sin(x-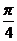 ),x∈R
),x∈R
的简图
解:列表
|
x |
-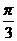 |
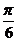 |
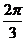 |
 |
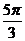 |
x+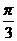 |
0 |
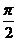 |
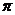 |
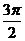 |
2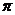 |
sin(x+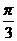 ) ) |
0 |
1 |
0 |
–1 |
0 |
描点画图:
|
x |
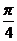 |
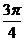 |
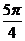 |
 |
 |
x-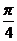 |
0 |
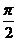 |
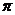 |
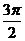 |
2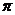 |
sin(x–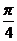 ) ) |
0 |
1 |
0 |
–1 |
0 |
通过比较,发现:

(1)函数y=sin(x+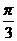 ),x∈R的图象可看作把正弦曲线上所有的点向左平行移动
),x∈R的图象可看作把正弦曲线上所有的点向左平行移动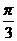 个单位长度而得到
个单位长度而得到
(2)函数y=sin(x-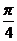 ),x∈R的图象可看作把正弦曲线上所有点向右平行移动
),x∈R的图象可看作把正弦曲线上所有点向右平行移动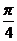 个单位长度而得到
个单位长度而得到
一般地,函数y=sin(x+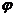 ),x∈R(其中
),x∈R(其中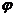 ≠0)的图象,可以看作把正弦曲线上所有点向左(当
≠0)的图象,可以看作把正弦曲线上所有点向左(当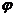 >0时)或向右(当
>0时)或向右(当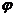 <0时=平行移动|
<0时=平行移动|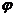 |个单位长度而得到
|个单位长度而得到 (用平移法注意讲清方向:“加左”“减右”)
(用平移法注意讲清方向:“加左”“减右”)
y=sin(x+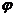 )与y=sinx的图象只是在平面直角坐标系中的相对位置不一样,这一变换称为相位变换
)与y=sinx的图象只是在平面直角坐标系中的相对位置不一样,这一变换称为相位变换
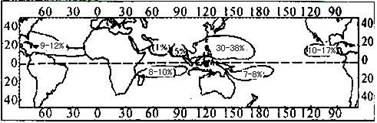
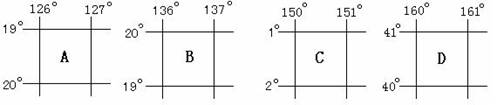
 (二)读“我国某地区沿某一纬线的地形剖面示意图”,判断回答4-6题。
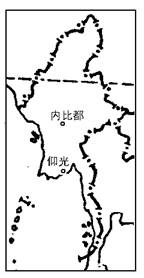
(二)读“我国某地区沿某一纬线的地形剖面示意图”,判断回答4-6题。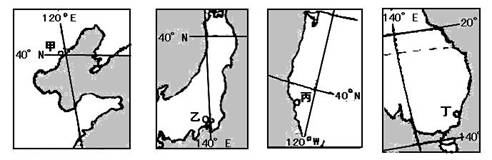
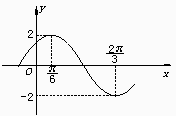
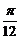 时,取得最大值2,当x=
时,取得最大值2,当x=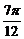 时取得最小值-2,那么( )
时取得最小值-2,那么( )
 2
2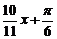 )
)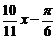 )
)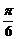 )
)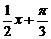 )在一个周期内的三个“零点”横坐标是( )
)在一个周期内的三个“零点”横坐标是( )
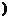 的最小值为-
的最小值为-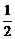 ,最大值为
,最大值为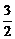 ,则a、b的值分别为________
,则a、b的值分别为________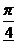 个单位得到的
个单位得到的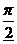 个单位得到的
个单位得到的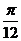 D
D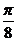 对称,则a=–1
对称,则a=–1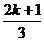 πx-
πx-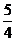 出现不少于4次且不多于8次,则k的值是( )
出现不少于4次且不多于8次,则k的值是( )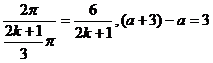
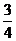 ≤T≤
≤T≤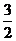 ,∴
,∴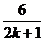 ≤
≤ ,∵k∈N,∴k=2或3
,∵k∈N,∴k=2或3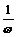 倍(纵坐标不变).若ω<0则可用诱导公式将符号“提出”再作图
倍(纵坐标不变).若ω<0则可用诱导公式将符号“提出”再作图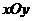 中,点P到两点
中,点P到两点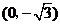 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为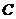 ,直线
,直线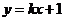 与C交于A,B两点.
与C交于A,B两点.
 ,求k的值;
,求k的值; 为焦点,长半轴为2的椭圆.它的短半轴
为焦点,长半轴为2的椭圆.它的短半轴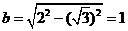 ,故方程为
,故方程为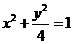 .
. 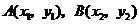 ,其坐标满足
,其坐标满足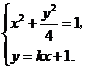
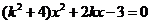 ,
,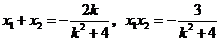 .若
.若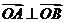 ,即
,即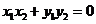 .
. ,于是
,于是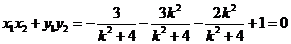 ,
,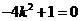 ,所以
,所以 .
. 
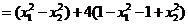
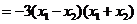
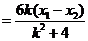 .
.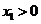 .由
.由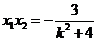 知
知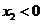 ,从而
,从而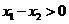 .又
.又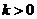 ,
,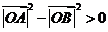 ,即在题设条件下,恒有
,即在题设条件下,恒有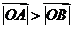 .
.