摘要：在直角坐标系中.点P到两点.的距离之和等于4.设点P的轨迹为.直线与C交于A.B两点． (Ⅰ)写出C的方程,(Ⅱ)若.求k的值, (Ⅲ)若点A在第一象限.证明:当k>0时.恒有||>||． 解:(Ⅰ)设P(x.y).由椭圆定义可知.点P的轨迹C是以为焦点.长半轴为2的椭圆．它的短半轴.故方程为． (Ⅱ)设.其坐标满足 消去y并整理得. 故．若.即． 而.于是. 化简得.所以． (Ⅲ) ． 因为A在第一象限.故．由知.从而．又. 故.即在题设条件下.恒有．
网址：http://m.1010jiajiao.com/timu_id_4393931[举报]
中，点P到两点
，
的距离之和等于4，设点P的轨迹为
，直线
与C交于A，B两点．
OB，求k的值在直角坐标系
中，点P到两点
，
的距离之和等于4，设点P的轨迹为
，直线
与C交于A，B两点．
（Ⅰ）写出C的方程；
（Ⅱ）若
，求
的值；
（Ⅲ）若点A在第一象限，证明：当
时，恒有||>||．
在直角坐标系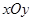
中，点P到两点
，
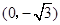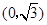的距离之和等于4，设点P的轨迹为
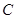，直线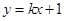
与C交于A，B两点． （Ⅰ）写出C的方程；（Ⅱ）若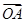
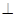
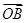，求k的值；
（Ⅲ）若点A在第一象限，证明：当k>0时，恒有||>||．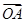
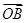查看习题详情和答案>>
中，点P到两点
，
的距离之和等于4，设点P的轨迹为
，直线
与C交于A，B两点．
，求k的值；
中，点P到两点
，
的距离之和等于4，设点P的轨迹为
，直线
与轨迹C交于A，B两点．
，求k的值；