18.(2009湖北卷理)(本小题满分14分)(注意：在试题卷上作答无效)

过抛物线的对称轴上一点的直线与抛物线相交于M、N两点，自M、N向直线作垂线，垂足分别为、。 　　　　　　

(Ⅰ)当时，求证：⊥；

(Ⅱ)记、 、的面积分别为、、，是否存在，使得对任意的，都有成立。若存在，求出的值；若不存在，说明理由。

20题。本小题主要考察抛物线的定义和几何性质等平面解析几何的基础知识，考查综合运用数学知识进行推理运算的能力。(14分)

解：依题意，可设直线MN的方程为，则有21世纪教育网　 　

由消去x可得 　　　　　　　　　　

从而有　　　　　　　　　　　　　　　　　　　　　　 　①

于是　　　　　　　　　　　　　　　　　 　②

又由，可得　　　　　　　　 　③

(Ⅰ)如图1，当时，点即为抛物线的焦点，为其准线

此时 ①可得

证法1：

　21世纪教育网　 　

证法2：

(Ⅱ)存在，使得对任意的，都有成立，证明如下：

证法1：记直线与x轴的交点为,则。于是有

将①、②、③代入上式化简可得

上式恒成立，即对任意成立 　　　　　　　　　

证法2：如图2，连接,则由可得

,所以直线经过原点O，

同理可证直线也经过原点O

又设则

17.(2009天津卷文)(本小题满分14分)

已知椭圆()的两个焦点分别为，过点的直线与椭圆相交于点A,B两点，且

(Ⅰ求椭圆的离心率

(Ⅱ)直线AB的斜率；

(Ⅲ)设点C与点A关于坐标原点对称，直线上有一点H(m,n)()在的外接圆上，求的值。

[答案](1)(2)(3)

[解析] (1)解：由，得,从而

，整理得，故离心率

(2)解：由(1)知，，所以椭圆的方程可以写为

设直线AB的方程为即

由已知设则它们的坐标满足方程组 21世纪教育网　 　

消去y整理，得

依题意，

而，有题设知，点B为线段AE的中点，所以

联立三式，解得，将结果代入韦达定理中解得

(3)由(2)知，，当时，得A由已知得

线段的垂直平分线l的方程为直线l与x轴的交点是的外接圆的圆心，因此外接圆的方程为

直线的方程为，于是点满足方程组由，解得，故

当时，同理可得

[考点定位]本小题主要考查椭圆的标准方程和几何性质，直线方程，圆的方程等基础知识。考查用代数方法研究圆锥曲线的性质和数形结合的思想，考查运算能力和推理能力。

16.(2009江西卷理)(本小题满分12分)

已知点为双曲线(为正常数)上任一点,为双曲线的右焦点,过作右准线的垂线,垂足为,连接并延长交轴于. 21世纪教育网　 　　　　

(1)　　 求线段的中点的轨迹的方程;

(2)　　 设轨迹与轴交于两点,在上任取一点,直线分别交轴于两点.求证:以为直径的圆过两定点.

解： (1) 由已知得,则直线的方程为:,

　 令得,即,

设,则,即代入得:,

即的轨迹的方程为. 21世纪教育网　 　　　　

(2) 在中令得,则不妨设,

于是直线的方程为:,直线的方程为:,

则,

则以为直径的圆的方程为: ,

令得:,而在上,则,

于是,即以为直径的圆过两定点.

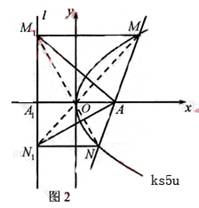
15.(2009江西卷文)(本小题满分14分)

如图，已知圆是椭圆的内接△的内切圆, 其中为椭圆的左顶点.　　　　　　

(1)求圆的半径;

(2)过点作圆的两条切线交椭圆于两点，

解: (1)设，过圆心作于,交长轴于

由得,

即　　 　　　　　　　(1)　　　　　　

而点在椭圆上,　　　 (2)

由(1)、 (2)式得,解得或(舍去)

(2) 设过点与圆相切的直线方程为:　　　　　　 (3)

则,即　　　　　　 (4)

解得

将(3)代入得,则异于零的解为

设,，则

则直线的斜率为：

于是直线的方程为:　

即

则圆心到直线的距离 　　　　　　21世纪教育网　 　

故结论成立.

14.(2009安徽卷文)(本小题满分12分)

已知椭圆(a＞b＞0)的离心率为，以原点为圆心。椭圆短半轴长半径的

圆与直线y=x+2相切，

(Ⅰ)求a与b；21世纪教育网　 　　　

(Ⅱ)设该椭圆的左，右焦点分别为和，直线过且与x轴垂直，动直线与y轴垂直，交与点p..求线段P垂直平分线与的交点M的轨迹方程，并指明曲线类型。

[思路](1)由椭圆建立a、b等量关系，再根据直线与椭圆相切求出a、b.

(2)依据几何关系转化为代数方程可求得，这之中的消参就很重要了。

[解析](1)由于　 ∴　 ∴　 又　 ∴b²=2,a²=3因此，. 21世纪教育网　 　　　

(2)由(1)知F₁，F₂两点分别为(-1，0)，(1,0)，由题意可设P(1，t).(t≠0).那么线段PF₁中点为，设M(x、y)是所求轨迹上的任意点.由于则消去参数t得

,其轨迹为抛物线(除原点)

13.(2009安徽卷理)(本小题满分13分)21世纪教育网　 　

点在椭圆上，直线与直线垂直，O为坐标原点，直线OP的倾斜角为，直线的倾斜角为.

(I)证明: 点是椭圆与直线的唯一交点； 　　　　

(II)证明:构成等比数列.

解：本小题主要考查直线和椭圆的标准方程和参数方程，直线和曲线的几何性质，等比数列等基础知识。考查综合运用知识分析问题、解决问题的能力。本小题满分13分。

解：(I)(方法一)由得代入椭圆,

得.

将代入上式,得从而

因此,方程组有唯一解,即直线与椭圆有唯一交点P. 　　　　　

(方法二)显然P是椭圆与的交点，若Q是椭圆与的交点，代入的方程，得

即故P与Q重合。

(方法三)在第一象限内，由可得

椭圆在点P处的切线斜率

切线方程为即。

因此，就是椭圆在点P处的切线。21世纪教育网　 　

根据椭圆切线的性质，P是椭圆与直线的唯一交点。

(II)的斜率为的斜率为

由此得构成等比数列。

12.(2009广东卷理)(本小题满分14分)

已知曲线与直线交于两点和，且．记曲线在点和点之间那一段与线段所围成的平面区域(含边界)为．设点是上的任一点，且点与点和点均不重合．

(1)若点是线段的中点，试求线段的中点的轨迹方程； 　　　　　　

(2)若曲线与有公共点，试求的最小值．

解：(1)联立与得，则中点，设线段的中点坐标为，则，即，又点在曲线上，

∴化简可得，又点是上的任一点，且不与点和点重合，则，即，∴中点的轨迹方程为().

　21世纪教育网　 　

(2)曲线，

即圆：，其圆心坐标为，半径

由图可知，当时，曲线与点有公共点；

当时，要使曲线与点有公共点，只需圆心到直线的距离，得，则的最小值为.

11.(2009全国卷Ⅱ文)(本小题满分12分)

已知椭圆C:　　　　　　　　　　 的离心率为　　　 ，过右焦点F的直线l与C相交于A、B

(Ⅰ)求a,b的值；

(Ⅱ)C上是否存在点P，使得当l绕F转到某一位置时，有成立？

若存在，求出所有的P的坐标与l的方程；若不存在，说明理由。

解析：本题考查解析几何与平面向量知识综合运用能力，第一问直接运用点到直线的距离公式以及椭圆有关关系式计算，第二问利用向量坐标关系及方程的思想，借助根与系数关系解决问题，注意特殊情况的处理。

解：(Ⅰ)设 当的斜率为1时，其方程为到的距离为

　 故　 ， 　21世纪教育网　 　

　　　 由

　　　 得 ，=

(Ⅱ)C上存在点，使得当绕转到某一位置时，有成立。

由 (Ⅰ)知C的方程为+=6. 设

　(ⅰ)

　C 成立的充要条件是， 且

整理得

故　　　 　　　　　　①

将

　21世纪教育网　 　

于是 , =,

　　 代入①解得，，此时

　　 于是=， 即 21世纪教育网　 　

　　 因此， 当时，， ；

　当时，， 。

(ⅱ)当垂直于轴时，由知，C上不存在点P使成立。

综上，C上存在点使成立，此时的方程为

.

10.(2009江苏卷)(本小题满分16分)

在平面直角坐标系中，已知圆和圆.

(1)若直线过点，且被圆截得的弦长为，求直线的方程；

(2)设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线和，它们分别与圆和圆相交，且直线被圆截得的弦长与直线被圆截得的弦长相等，试求所有满足条件的点P的坐标。

[解析] 本小题主要考查直线与圆的方程、点到直线的距离公式，考查数学运算求解能力、综合分析问题的能力。满分16分。

(1)设直线的方程为：，即

由垂径定理，得：圆心到直线的距离，

结合点到直线距离公式，得： 　　　

化简得：

求直线的方程为：或，即或

(2) 设点P坐标为，直线、的方程分别为：21世纪教育网　 　

，即：

因为直线被圆截得的弦长与直线被圆截得的弦长相等，两圆半径相等。由垂径定理，得：：圆心到直线与直线的距离相等。 　　

故有：，

化简得：

关于的方程有无穷多解，有： 　　　21世纪教育网　 　

解之得：点P坐标为或。

9. (2009山东卷文)(本小题满分14分)

设,在平面直角坐标系中,已知向量,向量,,动点的轨迹为E.

(1)求轨迹E的方程,并说明该方程所表示曲线的形状; 21世纪教育网　 　

(2)已知,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且(O为坐标原点),并求出该圆的方程;

(3)已知,设直线与圆C:(1<R<2)相切于A₁,且与轨迹E只有一个公共点B₁,当R为何值时,|A₁B₁|取得最大值?并求最大值.

解:(1)因为,,,

所以,　　 即. 21世纪教育网　 　

当m=0时,方程表示两直线,方程为;

当时, 方程表示的是圆

当且时,方程表示的是椭圆;

当时,方程表示的是双曲线.

(2).当时, 轨迹E的方程为,设圆心在原点的圆的一条切线为,解方程组得,即,

要使切线与轨迹E恒有两个交点A,B,

则使△=,

即,即,　　 且

,

要使, 　需使,即,

所以,　 即且,　 即恒成立.

所以又因为直线为圆心在原点的圆的一条切线,

所以圆的半径为,, 所求的圆为.

当切线的斜率不存在时,切线为,与交于点或也满足.

综上, 存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且.

(3)当时,轨迹E的方程为,设直线的方程为,因为直线与圆C:(1<R<2)相切于A₁, 由(2)知,　 即　　 ①,

因为与轨迹E只有一个公共点B₁,

由(2)知得,

即有唯一解

则△=, 　　即,　　 ②

由①②得,　 此时A,B重合为B₁(x₁,y₁)点, 21世纪教育网　 　

由 中,所以,,

B₁(x₁,y₁)点在椭圆上,所以,所以,

在直角三角形OA₁B₁中,因为当且仅当时取等号,所以,即

当时|A₁B₁|取得最大值,最大值为1.

[命题立意]:本题主要考查了直线与圆的方程和位置关系,以及直线与椭圆的位置关系,可以通过解方程组法研究有没有交点问题,有几个交点的问题.