11.(2009安徽卷文)(本小题满分12分)
某良种培育基地正在培育一种小麦新品种A，将其与原有的一个优良品种B进行对照
试验，两种小麦各种植了25亩，所得亩产数据(单位：千克)如下：. 
品种A:357，359，367，368，375，388，392，399，400，405，414，
415，421，423，423，427，430，430，434，443，445，451，454
品种B：363，371，374，383，385，386，391，392，394，395，397
397，400，401，401，403，406，407，410，412，415，416，422，430
(Ⅰ)完成所附的茎叶图
(Ⅱ)用茎叶图处理现有的数据，有什么优点？.
(Ⅲ)通过观察茎叶图，对品种A与B的亩产量及其稳定性进行比较，写出统计结论。
[思路]由统计知识可求出A、B两种品种的小麦稳定性大小并画出茎叶图，用茎叶图处理数据，看其分布就比较明了。.
[解析](1)茎叶图如图所示
|
A |
|
B |
|
9 7 |
35 |
|
|
8 7 |
36 |
3 |
|
5 |
37 |
1 4 |
|
8 |
38 |
3 5 6 |
|
9 2 |
39 |
1 2 4 457 7 |
|
5 0 |
40 |
0 1 1 3 6 7 |
|
5 4 2 |
41 |
0 2 5 6 |
|
7 3 3 1 |
42 |
2 |
|
4 0 0 |
43 |
0 |
|
5 5 3 |
44 |
|
|
4 1 |
45 |
|
(2)用茎叶图处理现有的数据不仅可以看出数据的分布状况,而且可以看出每组中的具体数据.
(3)通过观察茎叶图，可以发现品种A的平均每亩产量为411.1千克，品种B的平均亩产量为397.8千克.由此可知,品种A的平均亩产量比品种B的平均亩产量高.但品种A的亩产量不够稳定，而品种B的亩产量比较集中D平均产量附近.
10.(2009安徽卷理)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感，其中只有A到过疫区.B肯定是受A感染的.对于C，因为难以断定他是受A还是受B感染的，于是假定他受A和受B感染的概率都是
.同样也假定D受A、B和C感染的概率都是
.在这种假定之下，B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
本小题主要考查古典概型及其概率计算，考查取有限个值的离散型随机变量及其分布列和均值的概念，通过设置密切贴近现实生活的情境，考查概率思想的应用意识和创新意识。体现数学的科学价值。本小题满分12分。
解：随机变量X的分布列是
|
X |
1 |
2 |
3 |
|
P |
|
|
|
X的均值为
附：X的分布列的一种求法
共有如下6种不同的可能情形，每种情形发生的概率都是：
|
① |
② |
③ |
④ |
⑤ |
⑥ |
|
A-B-C-D |
A-B-C └D |
A-B-C └D |
A-B-D └C |
A-C-D └B |
 |
在情形①和②之下，A直接感染了一个人；在情形③、④、⑤之下，A直接感染了两个人；在情形⑥之下，A直接感染了三个人。
表示事件：从甲组抽取的工人中恰有1名女工人，则
表示事件：从甲组抽取的2名工人中恰有
表示事件：从乙组抽取的2名工人中恰有
名男工人，
独立，
，且
7.(2009山东卷文)(本小题满分12分)
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
z |
|
标准型 |
300 |
450 |
600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1) 求z的值.
(2) 用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3) 用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
解: (1).设该厂本月生产轿车为n辆,由题意得,
,所以n=2000. z=2000-100-300-150-450-600=400
(2) 设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,所以
,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1, B1), (S1, B2) , (S1,
B3) (S2 ,B1), (S2 ,B2), (S2
,B3),( (S1, S2),(B1 ,B2),
(B2 ,B3) ,(B1 ,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件: (S1, B1),
(S1, B2) , (S1, B3) (S2 ,B1),
(S2 ,B2), (S2 ,B3),( (S1,
S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为
.
(3)样本的平均数为
,
那么与样本平均数之差的绝对值不超过0.5的数为9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为
.
[命题立意]:本题为概率与统计的知识内容,涉及到分层抽样以及古典概型求事件的概率问题.要读懂题意,分清类型,列出基本事件,查清个数.,利用公式解答.
6.(2009山东卷理)(本小题满分12分)
在某校组织的一次篮球定点投篮训练中，规定每人最多投3次；在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次，某同学在A处的命中率q
为0.25，在B处的命中率为q
，该同学选择先在A处投一球，以后都在B处投，用
表示该同学投篮训练结束后所得的总分，其分布列为
|
|
0
|
2
|
3 |
4 |
5 |
|
p
|
0.03
|
P1
|
P2 |
P3
|
P4
|
(1) 求q的值；
(2) 求随机变量的数学期望E;
(3) 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
解:(1)设该同学在A处投中为事件A,在B处投中为事件B,则事件A,B相互独立,且P(A)=0.25,
,
P(B)= q,
.
根据分布列知: =0时
=0.03,所以
，q=0.8.
(2)当=2时, P1=
=0.75 q(
)×2=1.5 q(
)=0.24
当=3时, P2 ==0.01,
当=4时, P3=
=0.48,
当=5时, P4=
=0.24
所以随机变量的分布列为
|
|
0
|
2
|
3 |
4 |
5 |
|
p
|
0.03
|
0.24
|
0.01 |
0.48
|
0.24
|
随机变量的数学期望
(3)该同学选择都在B处投篮得分超过3分的概率为
;
该同学选择(1)中方式投篮得分超过3分的概率为0.48+0.24=0.72.
由此看来该同学选择都在B处投篮得分超过3分的概率大.
[命题立意]:本题主要考查了互斥事件的概率,相互独立事件的概率和数学期望,以及运用概率知识解决问题的能力.
.
”等价于事件“该学生在路上遇到
次红灯”(
0，1，2，3，4)，
，
.
.
，
.
.3.(2009浙江卷理)(本题满分14分)在
这
个自然数中，任取个数．
(I)求这个数中恰有
个是偶数的概率；
(II)设为这个数中两数相邻的组数(例如：若取出的数为
，则有两组相邻的数
和
，此时的值是
)．求随机变量的分布列及其数学期望．
解析：(I)记“这3个数恰有一个是偶数”为事件A，则
；.
(II)随机变量的取值为
的分布列为
|
|
0 |
1 |
2 |
|
P |
|
|
|
所以的数学期望为
.
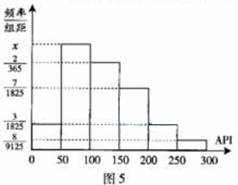
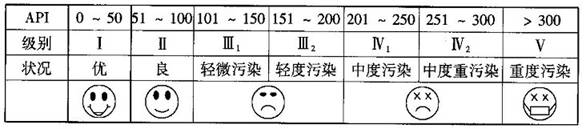对某城市一年(365天)的空气质量进行监测，获得的API数据按照区间
，
，
，
，
，
的值； 
，
，
，
)
；
，则空气质量不为良且不为轻微污染的概率为
，一周至少有两天空气质量为良或轻微污染的概率为
.