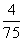1.依次填入下面一段话中画线处的标点,恰当的一组是
“画人画鬼高人一等,刺贪刺虐入骨三分” ① 这是郭沫若为蒲松龄纪念馆聊斋堂写的对联。“画人画鬼”,指《聊斋志异》的题材内容 ② 它借狐鬼故事来达到“刺贪刺虐”的目的;“高人一等”,是评价蒲松龄在文学史上的贡献;“入骨三分”,则概括了他在创作上的成就。今天这节课要学习他的名篇 ③ 促织,让我们来看看这个评价是否恰当 ④
|
|
① |
② |
③ |
④ |
|
A |
, |
, |
《
》 |
。 |
|
B |
。 |
; |
“
” |
。 |
|
C |
。 |
; |
《
》 |
? |
|
D |
。 |
, |
“
” |
? |
(16)(本小题满分12分)在 ABC中,C-A=
ABC中,C-A=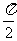 , sinB=
, sinB=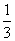 。
。
(I)求sinA的值;
(II)设AC=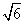 ,求
,求 ABC的面积。
ABC的面积。
(16)本小题主要考查三角恒等变换、正弦定理、解三角形等有关知识,考查运算求解能力。本小题满分12分
解:(I)由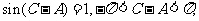 知
知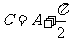 。
。
又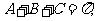 所以
所以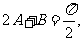 即
即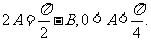
故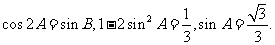
(II)由(I)得: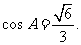
又由正弦定理,得: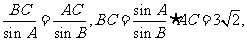
所以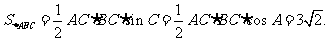
(17)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区。B肯定是受A感染的。对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是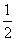 。同样也假定D受A、B和C感染的概率都是
。同样也假定D受A、B和C感染的概率都是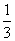 。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
(17)本小题主要考查古典概型及其概率计算,考查取有限个值的离散型随机变量及其分布列和均值的概念,通过设置密切贴近现实生活的情境,考查概率思想的应用意识和创新意识。体现数学的科学价值。本小题满分12分。
|
X |
1 |
2 |
3 |
|
P |
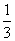 |
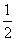 |
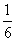 |
解:随机变量X的分布列是
X的均值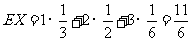 。
。
附:X的分布列的一种求法
共有如下6种不同的可能情形,每种情形发生的概率都是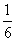 :
:
|
① |
② |
③ |
④ |
⑤ |
⑥ |
|
A-B-C-D |
A-B-C └D |
A-B-C └D |
A-B-D └C |
A-C-D └B |
 |
在情形①和②之下,A直接感染了一个人;在情形③、④、⑤之下,A直接感染了两个人;在情形⑥之下,A直接感染了三个人。
 (18)(本小题满分13分)
(18)(本小题满分13分)
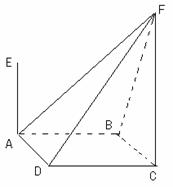
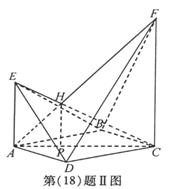
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,
BD=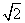 ,AE、CF都与平面ABCD垂直,AE=1,CF=2。
,AE、CF都与平面ABCD垂直,AE=1,CF=2。
(I)求二面角B-AF-D的大小;
(II)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积。
(18) 本小题主要考查直线与直线、直线与平面、平面与平面的位置关系、相交平面所成二面角以及空间几何体的体积计算等知识,考查空间想象能力和推理论证能力、利用综合法或向量法解决立体几何问题的能力。本小题满分13分。
解:(I)(综合法)连接AC、BD交于菱形的中心O,过O作OG⊥AF,G为垂足。连接BG、DG。
由BD⊥AC,BD⊥CF,得:BD⊥平面ACF,故BD⊥AF.
于是AF⊥平面BGD,所以BG⊥AF,DG⊥AF,∠BGD为二面角B-AF-D的平面角。
由FC⊥AC,FC=AC=2,得∠FAC=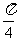 ,OG=
,OG=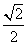 .
.
由OB⊥OG,OB=OD=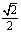 ,得∠BGD=2∠BGO=
,得∠BGD=2∠BGO=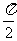 .
.
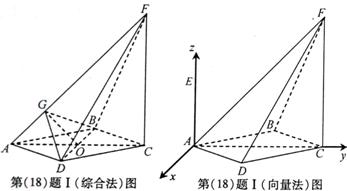
(向量法)以A为坐标原点,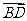 、
、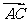 、
、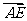 方向分别为
方向分别为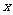 轴、
轴、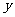 轴、
轴、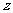 轴的正方向建立空间直角坐标系(如图).于是
轴的正方向建立空间直角坐标系(如图).于是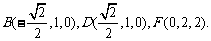
设平面ABF的法向量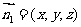 ,则由
,则由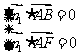 得
得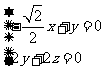 。
。
令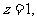 得
得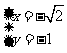 ,
,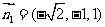
同理,可求得平面ADF的法向量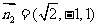 。
。
由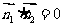 知,平面ABF与平面ADF垂直,
知,平面ABF与平面ADF垂直,
二面角B-AF-D的大小等于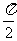 。
。
(II)连EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD。
过H作HP⊥平面ABCD,P为垂足。
因为EA⊥平面ABCD,FC⊥平面ABCD,,所以平面ACFE⊥平面ABCD,从而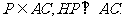
由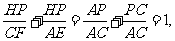 得
得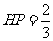 。
。
又因为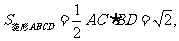
故四棱锥H-ABCD的体积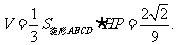
(19)(本小题满分12分)
已知函数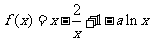 ,a>0,讨论
,a>0,讨论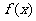 的单调性.
的单调性.
(19)本小题主要考查函数的定义域、利用导数等知识研究函数的单调性,考查分类讨论的思想方法和运算求解的能力。本小题满分12分。
解: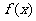 的定义域是(0,+
的定义域是(0,+ ),
),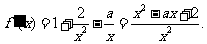
设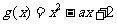 ,二次方程
,二次方程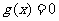 的判别式
的判别式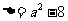 .
.
① 当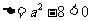 ,即
,即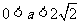 时,对一切
时,对一切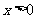 都有
都有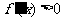 ,此时
,此时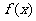 在
在 上是增函数。
上是增函数。
② 当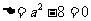 ,即
,即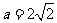 时,仅对
时,仅对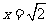 有
有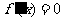 ,对其余的
,对其余的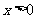 都有
都有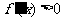 ,此时
,此时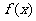 在
在 上也是增函数。
上也是增函数。
③ 当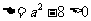 ,即
,即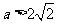 时,
时,
方程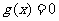 有两个不同的实根
有两个不同的实根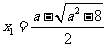 ,
,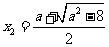 ,
,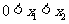 .
.
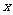 |
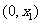 |
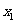 |
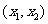 |
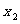 |
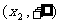 |
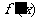 |
+ |
0 |
_ |
0 |
+ |
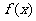 |
单调递增 |
极大 |
单调递减 |
极小 |
单调递增 |
此时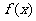 在
在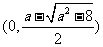 上单调递增, 在
上单调递增, 在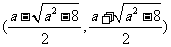 是上单调递减, 在
是上单调递减, 在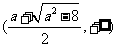 上单调递增.
上单调递增.
(20)(本小题满分13分)
点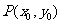 在椭圆
在椭圆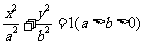 上,
上,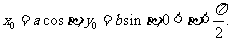 直线
直线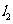 与直线
与直线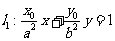 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为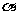 ,直线
,直线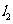 的倾斜角为
的倾斜角为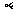 .
.
(I)证明: 点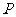 是椭圆
是椭圆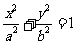 与直线
与直线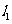 的唯一交点;
的唯一交点;
(II)证明: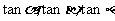 构成等比数列。
构成等比数列。
(20)本小题主要考查直线和椭圆的标准方程和参数方程,直线和曲线的几何性质,等比数列等基础知识。考查综合运用知识分析问题、解决问题的能力。本小题满分13分。
解:(I)(方法一)由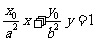 得
得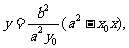 代入椭圆
代入椭圆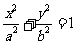 ,
,
得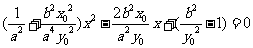 .
.
将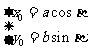 代入上式,得
代入上式,得 从而
从而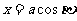
因此,方程组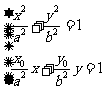 有唯一解
有唯一解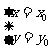 ,即直线
,即直线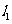 与椭圆有唯一交点P.
与椭圆有唯一交点P.
(方法二)显然P是椭圆与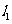 的交点,若Q
的交点,若Q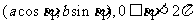 是椭圆与
是椭圆与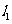 的交点,代入
的交点,代入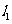 的方程
的方程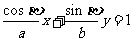 ,得
,得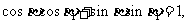
即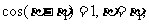 故P与Q重合。
故P与Q重合。
(方法三)在第一象限内,由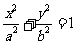 可得
可得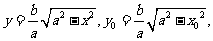
椭圆在点P处的切线斜率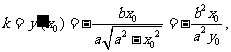
切线方程为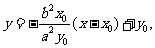 即
即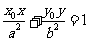 。
。
因此,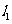 就是椭圆在点P处的切线。
就是椭圆在点P处的切线。
根据椭圆切线的性质,P是椭圆与直线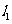 的唯一交点。
的唯一交点。
(II)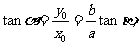
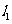 的斜率为
的斜率为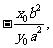
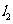 的斜率为
的斜率为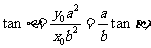
由此得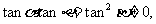
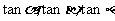 构成等比数列。
构成等比数列。
(21)(本小题满分13分)
首项为正数的数列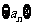 满足
满足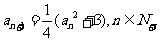
(I)证明:若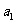 为奇数,则对一切
为奇数,则对一切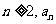 都是奇数;
都是奇数;
(II)若对一切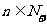 都有
都有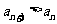 ,求
,求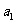 的取值范围。
的取值范围。
(21)本小题主要考查数列、数学归纳法和不等式的有关知识,考查推理论证、抽象概括、运算求解和探究能力,考查学生是否具有审慎思维的习惯和一定的数学视野。本小题满分13分。
解:(I)已知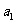 是奇数,假设
是奇数,假设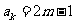 是奇数,其中
是奇数,其中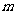 为正整数,
为正整数,
则由递推关系得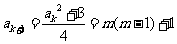 是奇数。
是奇数。
根据数学归纳法,对任何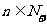 ,
,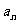 都是奇数。
都是奇数。
(II)(方法一)由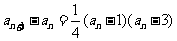 知,
知,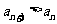 当且仅当
当且仅当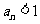 或
或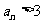 。
。
另一方面,若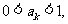 则
则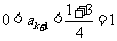 ;若
;若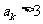 ,则
,则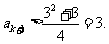
根据数学归纳法,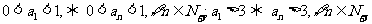
综合所述,对一切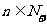 都有
都有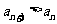 的充要条件是
的充要条件是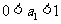 或
或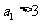 。
。
(方法二)由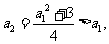 得
得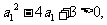 于是
于是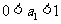 或
或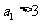 。
。
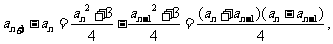
因为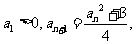 所以所有的
所以所有的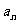 均大于0,因此
均大于0,因此 与
与 同号。
同号。
根据数学归纳法,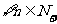 ,
, 与
与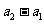 同号。
同号。
因此,对一切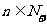 都有
都有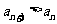 的充要条件是
的充要条件是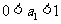 或
或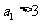 。
。
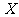 -
-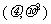 ,则
,则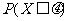 =________.
=________.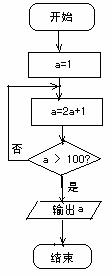 (12)以直角坐标系的原点为极点,
(12)以直角坐标系的原点为极点,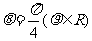 ,它与曲线
,它与曲线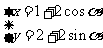 (
(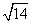
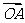 和
和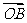 ,它们的夹角为
,它们的夹角为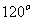 .如图所示,点C在以O为圆心的圆弧AB上变动.若
.如图所示,点C在以O为圆心的圆弧AB上变动.若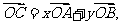 其中
其中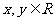 ,则
,则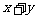 的最大值是=________.
的最大值是=________.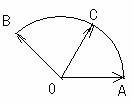 2
2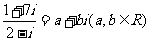 ,则乘积
,则乘积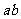 的值是(B)
的值是(B)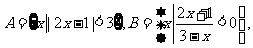 则A∩B是(D)
则A∩B是(D)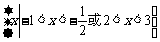 (B)
(B) 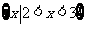
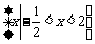 (D)
(D) 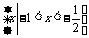
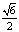 的是(B)
的是(B)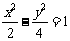 (B)
(B)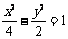 (C)
(C)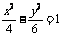 (D)
(D)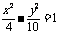
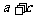 >b+d , q:
>b+d , q: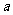 >b且c>d
>b且c>d
 的图像不过第二象限
的图像不过第二象限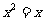
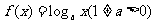 在
在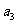 +
+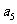 =105,
=105,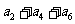 =99,以
=99,以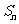 表示
表示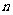 项和,则使得
项和,则使得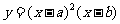 的图像可能是(C)
的图像可能是(C)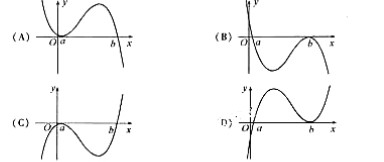
 所表示的平面区域被直线
所表示的平面区域被直线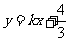 分为面积相等的两部分,则
分为面积相等的两部分,则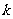 的值是(A) (A)
的值是(A) (A)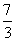 (B)
(B)
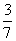 (C)
(C)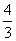 (D)
(D) 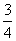
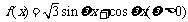 ,
,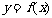 的图像与直线
的图像与直线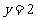 的两个相邻交点的距离等于
的两个相邻交点的距离等于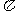 ,则
,则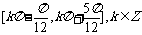 (B)
(B)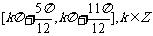
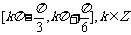 (D)
(D)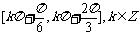
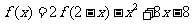 ,则曲线
,则曲线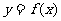 在点
在点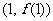 处的切线方程是(A)
处的切线方程是(A)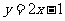 (B)
(B)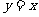 (C)
(C)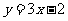 (D)
(D)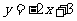
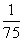 (B)
(B) 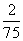 (C)
(C)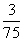 (D)
(D)