摘要:已知函数在处有极值. (Ⅰ)求实数值, (Ⅱ)求函数的单调区间, (Ⅲ)试问是否存在实数.使得不等式对任意 及 恒成立?若存在.求出的取值范围,若不存在.请说明理由. 解:(Ⅰ)因为. 所以. --2分 由.可得 .. 经检验时.函数在处取得极值. 所以. ---4分 (Ⅱ). . --6分 而函数的定义域为. 当变化时..的变化情况如下表: - 0 + ↘ 极小值 ↗ 由表可知.的单调减区间为.的单调减区间为.--9分 (3)∵.时. -10分 不等式对任意 及恒成立.即 . 即对恒成立. -12分 令.. 解得为所求. -14分
网址:http://m.1010jiajiao.com/timu_id_3935641[举报]
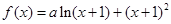 在
在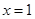 处有极值.
处有极值.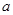 值;
值;
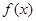 的单调区间;
的单调区间;
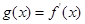 ,若曲线
,若曲线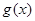 在
在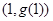 处的切线与两坐标轴分别交于
处的切线与两坐标轴分别交于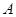 ,
,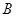 两点(
两点(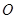 为坐标原点),求
为坐标原点),求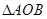 的面积.
的面积.
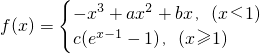 在
在 处取到极值
处取到极值 恰有三个实根,求实数k的取值范围;
恰有三个实根,求实数k的取值范围; (O为坐标原点),且线段AB的中点在y轴上,求实数c的取值范围.
(O为坐标原点),且线段AB的中点在y轴上,求实数c的取值范围. 在
在 处取到极值
处取到极值 恰有三个实根,求实数k的取值范围;
恰有三个实根,求实数k的取值范围; (O为坐标原点),且线段AB的中点在y轴上,求实数c的取值范围.
(O为坐标原点),且线段AB的中点在y轴上,求实数c的取值范围.