摘要：已知函数 (Ⅰ)求函数的极大值, (Ⅱ)若时.恒有成立(其中是函数的导函数).试确定实数的取值范围． (Ⅰ).且. -------------1分 当时.得, 当时.得, ∴的单调递增区间为, 的单调递减区间为和． ------------5分 故当时.有极大值.其极大值为． ------6分 (Ⅱ). ⅰ)当时.即时. 在区间内单调递减． ∴． ∵.∴． 此时.． ------------------------9分 ⅱ)当.且时.即. ． ∵.∴即 ∴ ∴． 此时.． ------------------12分 ⅲ)当时.得与已知矛盾． ------13分 综上所述.实数的取值范围为． ---------14分
网址：http://m.1010jiajiao.com/timu_id_3935647[举报]
已知函数
和函数g（x）=lnx，记F（x）=f（x）+g（x）．
（1）当
时，若f（x）在[1，2]上的最大值是f（2），求实数a的取值范围；
（2）当a=1时，判断F（x）在其定义域内是否有极值，并予以证明；
（3）对任意的
，若F（x）在其定义域内既有极大值又有极小值，试求实数a的取值范围．
查看习题详情和答案>>
和函数g（x）=lnx，记F（x）=f（x）+g（x）．（1）当
时，若f（x）在[1，2]上的最大值是f（2），求实数a的取值范围；（2）当a=1时，判断F（x）在其定义域内是否有极值，并予以证明；
（3）对任意的
，若F（x）在其定义域内既有极大值又有极小值，试求实数a的取值范围．查看习题详情和答案>>
已知函数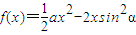
和函数g（x）=lnx，记F（x）=f（x）+g（x）．
（1）当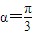
时，若f（x）在[1，2]上的最大值是f（2），求实数a的取值范围；
（2）当a=1时，判断F（x）在其定义域内是否有极值，并予以证明；
（3）对任意的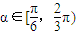
，若F（x）在其定义域内既有极大值又有极小值，试求实数a的取值范围．
查看习题详情和答案>>
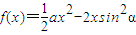和函数g（x）=lnx，记F（x）=f（x）+g（x）．（1）当
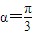时，若f（x）在[1，2]上的最大值是f（2），求实数a的取值范围；（2）当a=1时，判断F（x）在其定义域内是否有极值，并予以证明；
（3）对任意的
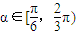，若F（x）在其定义域内既有极大值又有极小值，试求实数a的取值范围．查看习题详情和答案>>
已知函数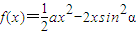
和函数g（x）=lnx，记F（x）=f（x）+g（x）．
（1）当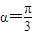
时，若f（x）在[1，2]上的最大值是f（2），求实数a的取值范围；
（2）当a=1时，判断F（x）在其定义域内是否有极值，并予以证明；
（3）对任意的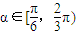
，若F（x）在其定义域内既有极大值又有极小值，试求实数a的取值范围．
查看习题详情和答案>>
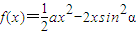和函数g（x）=lnx，记F（x）=f（x）+g（x）．（1）当
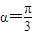时，若f（x）在[1，2]上的最大值是f（2），求实数a的取值范围；（2）当a=1时，判断F（x）在其定义域内是否有极值，并予以证明；
（3）对任意的
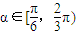，若F（x）在其定义域内既有极大值又有极小值，试求实数a的取值范围．查看习题详情和答案>>
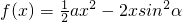和函数g（x）=lnx，记F（x）=f（x）+g（x）．
时，若f（x）在[1，2]上的最大值是f（2），求实数a的取值范围；
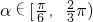，若F（x）在其定义域内既有极大值又有极小值，试求实数a的取值范围．
和函数
，记
．
时，若
在
上的最大值是
，求实数
的取值范围；
时，判断
在其定义域内是否有极值，并予以证明；
，若