摘要: 已知函数在与处都取得极值. (Ⅰ)求的值及函数的单调区间, (Ⅱ)若对.不等式恒成立.求的取值范围. 分析:利用分离变量法求参数 解:(Ⅰ).由题意: 即 解得 ∴. 令.解得, 令.解得或. ∴的减区间为,增区间为..---------------5分 知.在上单调递增, 在上单调递减, 在上单调递增. ∴时.的最大值即为与中的较大者. , ∴当时.取得最大值. 要使.只需.即: 解得:或. ∴的取值范围为. -------------14分
网址:http://m.1010jiajiao.com/timu_id_3935642[举报]
 在
在 与
与 处都取得极值.
处都取得极值. 的解析式;
的解析式;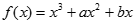 在
在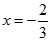 与
与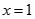 处都取得极值.
处都取得极值.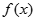 的解析式;
的解析式;