题目内容
9.太空中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其它星体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行.设这三个星体的质量均为M,并设两种系统的运动周期相同,则下列说法不正确的是( )
| A. | 直线三星系统中甲星和丙星的角速度相同 | |
| B. | 此三星系统的运动周期为T=4πR$\sqrt{\frac{R}{5GM}}$ | |
| C. | 三角形三星系统中星体间的距离为L=$\root{3}{{\frac{12}{5}}}$R | |
| D. | 三角形三星系统的线速度大小为$\frac{1}{2}$$\sqrt{\frac{5GM}{R}}$ |
分析 明确研究对象,对研究对象受力分析,找到做圆周运动所需向心力的来源,结合牛顿第二定律列式分析
解答 解:A、直线三星系统中甲星和丙星绕着乙星做匀速圆周运动,由于质量都相等,甲星和丙星所受万有引力的合力相等,根据$F=M{ω}_{\;}^{2}R$知故直线三星系统中甲星和丙星的角速度相同,故A正确;
B、三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;其中边上的一颗星受中央星和另一颗边上星的万有引力提供向心力.
$G\frac{{M}_{\;}^{2}}{{R}_{\;}^{2}}+G\frac{{M}_{\;}^{2}}{(2R)_{\;}^{2}}=M\frac{{v}_{\;}^{2}}{R}$,解得:$v=\sqrt{\frac{5GM}{4R}}$,$T=\frac{2πR}{v}=4πR\sqrt{\frac{R}{5GM}}$,故B正确
C、另一种形式是三颗星位于等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行,由万有引力定律和牛顿第二定律得$2G\frac{{M}_{\;}^{2}}{{L}_{\;}^{2}}cos30°=M\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}\frac{\frac{L}{2}}{cos30°}$
由于两种系统的运动周期相同,即$T=4πR\sqrt{\frac{R}{5GM}}$,故解得:$L=\root{3}{\frac{12}{5}}R$,故C正确;
D、根据$v=\frac{2πR}{T}=\frac{2π}{T}(\frac{L}{2cos30°})=\root{3}{\frac{12}{5}}•\frac{1}{2}\sqrt{\frac{5GM}{R}}$,故D错误
本题选错误的,故选:D
点评 万有引力定律和牛顿第二定律是力学的重点,在本题中有些同学找不出什么力提供向心力,关键在于进行正确受力分析.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | $\frac{{4{π^2}{r^3}}}{{G{T^2}}}$ | B. | $\frac{{3π{R^3}}}{{G{T^2}{r^3}}}$ | C. | $\frac{{3π{r^3}}}{{G{T^2}{R^3}}}$ | D. | $\frac{3π}{{G{T^2}}}$ |
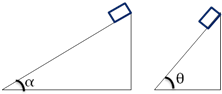 如图所示,两个质量相同的物体从同一高度沿倾角不同的两个光滑斜面由静止滑下,到达斜面底端的过程中,两物体相同的物理量为( )
如图所示,两个质量相同的物体从同一高度沿倾角不同的两个光滑斜面由静止滑下,到达斜面底端的过程中,两物体相同的物理量为( )| A. | 重力的冲量 | B. | 弹力的冲量 | ||
| C. | 合外力的冲量 | D. | 动量改变量的大小 |
 国际乒联为使乒乓球在比赛中的来回次数增加,提高比赛的观赏性,将比赛用球的直径从原来的38mm增大到40mm,质量由原来的2.5克增加到2.7克.研究人员称,40mm大球比原38mm小球旋转减弱$\frac{1}{5}$,速度减慢$\frac{1}{7}$,弹性也有所下降.小李为了比较新、老标准乒乓球的运动特性,他请另一同学将一只直径40mm的大球和一只直径38mm的小球,从同一高处同时自由落下,在两球下落过程中,他用照相机拍摄到两球下落过程中一段径迹的照片,如图所示,背景中的横虚线是竖直墙面上两块磁砖的接逢处.拍摄时所用快门速度为$\frac{1}{30}$秒,则:
国际乒联为使乒乓球在比赛中的来回次数增加,提高比赛的观赏性,将比赛用球的直径从原来的38mm增大到40mm,质量由原来的2.5克增加到2.7克.研究人员称,40mm大球比原38mm小球旋转减弱$\frac{1}{5}$,速度减慢$\frac{1}{7}$,弹性也有所下降.小李为了比较新、老标准乒乓球的运动特性,他请另一同学将一只直径40mm的大球和一只直径38mm的小球,从同一高处同时自由落下,在两球下落过程中,他用照相机拍摄到两球下落过程中一段径迹的照片,如图所示,背景中的横虚线是竖直墙面上两块磁砖的接逢处.拍摄时所用快门速度为$\frac{1}{30}$秒,则: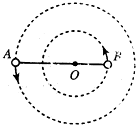 神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.
神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T. 温度传感器广泛应用于家用电器中,它是利用热敏电阻的阻值随温度变化的特性来工作的.如图甲所示为某装置中的传感器工作原理图,已知电源的电动势E=9.0V,内阻不计;G为灵敏电流表,其内阻Rg保持不变;R为热敏电阻,其阻值随温度的变化关系如图乙所示,闭合开关S,当R的温度等于20℃时,电流表示数I1=2mA;当电流表的示数I2=3.6mA时,热敏电阻的温度是120℃.
温度传感器广泛应用于家用电器中,它是利用热敏电阻的阻值随温度变化的特性来工作的.如图甲所示为某装置中的传感器工作原理图,已知电源的电动势E=9.0V,内阻不计;G为灵敏电流表,其内阻Rg保持不变;R为热敏电阻,其阻值随温度的变化关系如图乙所示,闭合开关S,当R的温度等于20℃时,电流表示数I1=2mA;当电流表的示数I2=3.6mA时,热敏电阻的温度是120℃.