题目内容
17.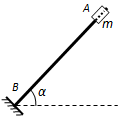 如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆上各处与滑块之间的动摩擦因素保持不变,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,滑块与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,下列说法中正确的是( )
如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆上各处与滑块之间的动摩擦因素保持不变,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,滑块与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,下列说法中正确的是( )| A. | 可以求出滑块下滑和上滑过程加速度的大小a1、a2 | |
| B. | 取过B点的水平面为零势能面,则可以判断滑块从A下滑至B的过程中,重力势能等于动能的位置在AB中点的下方 | |
| C. | 可以求出滑块在杆上运动的总路程S | |
| D. | 可以求出滑块第一次与挡板碰撞时重力做功的瞬时功率P |
分析 滑块运动分两个阶段,匀加速下滑和匀减速上滑,利用牛顿第二定律求出两端加速度,利用运动学公式求解加速度;
在求解总路程时,可以用动能定理全程列式求解.
解答 解:A、设下滑位移为L,到达底端速度为v
由公式v2=2ax得:
下滑过程:v2=2a2L ①
上滑过程:v2=2a1$\frac{L}{2}$=a1L ②
由牛顿第二定律得:
下滑加速度为:a2=$\frac{mgsinα-f}{m}$③
上滑加速度为:a1=$\frac{mgsinα+f}{m}$④
①②③④联立得:a2=$\frac{2gsinα}{3}$,a1=$\frac{4gsinα}{3}$,故A正确;
B、可以考虑到达AB中点时刻,如果没有摩擦,则机械能守恒,此时动能与重力势能相等;但实际有摩擦,动能偏小,故需要继续下降才可能动能和势能相等,故B正确;
C、将滑块拉到A点由静止释放能够下滑,说明重力的下滑分力大于最大静摩擦力,故最终滑块停在底端;
对运动全程,根据动能定理,有:mgLsinα-μmgcosα•S=0-0,
对从释放到第一次反弹到最高点过程,根据动能定理,有:mg$\frac{L}{2}$sinα-μmgcosα•$\frac{3}{2}L$=0-0,
联立解得:S=$\frac{3L}{tanα}$,不知道L,故C错误;
D、由于不知道杆的长度L,故滑块第一次与挡板碰撞时的速度无法求解,也就不能求解此时重力的瞬时功率,故D错误;
故选:AB
点评 解决本题的关键是上滑和下滑时摩擦力方向不同,所以加速度不同,另外抓住连接两段的桥梁是碰撞前后速度大小相等;在不涉及加速度时,可以根据动能定理列式判断.

练习册系列答案
相关题目
7.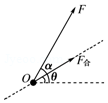 某科研单位设计了一空间飞行器,飞行器从地面静止起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰好与水平方向成θ=30°角的直线斜向右上方匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
某科研单位设计了一空间飞行器,飞行器从地面静止起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰好与水平方向成θ=30°角的直线斜向右上方匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
 某科研单位设计了一空间飞行器,飞行器从地面静止起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰好与水平方向成θ=30°角的直线斜向右上方匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
某科研单位设计了一空间飞行器,飞行器从地面静止起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰好与水平方向成θ=30°角的直线斜向右上方匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )| A. | 加速时加速度的大小为g | B. | 加速时动力的大小等于mg | ||
| C. | 减速时动力的大小$\frac{1}{2}$mg | D. | 减速飞行时间2t后速度为零 |
8.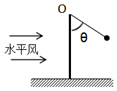 如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v的大小成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=60°,则( )
如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v的大小成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=60°,则( )
 如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v的大小成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=60°,则( )
如图是简易测水平风速的装置,轻质塑料球用细线悬于竖直杆顶端O,当水平风吹来时,球在水平风力F的作用下飘起来.F与风速v的大小成正比,当v=3m/s时,测得球平衡时细线与竖直方向的夹角θ=60°,则( )| A. | 水平风力F越大,球平衡时,细线所受拉力越小 | |
| B. | 当风速v=3 m/s时,F的大小恰好等于球的重力的$\sqrt{3}$倍 | |
| C. | 当风速v=6 m/s时,θ=90° | |
| D. | 换用半径相等,但质量较小的球,则当θ=60°时,v大于3m/s |
5.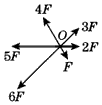 如图所示,在同一平面内有六个共点力,大小分别为F、2F、3F、4F、5F、6F,相邻的两个力之间的夹角均为60°,则它们合力的大小和方向是( )
如图所示,在同一平面内有六个共点力,大小分别为F、2F、3F、4F、5F、6F,相邻的两个力之间的夹角均为60°,则它们合力的大小和方向是( )
 如图所示,在同一平面内有六个共点力,大小分别为F、2F、3F、4F、5F、6F,相邻的两个力之间的夹角均为60°,则它们合力的大小和方向是( )
如图所示,在同一平面内有六个共点力,大小分别为F、2F、3F、4F、5F、6F,相邻的两个力之间的夹角均为60°,则它们合力的大小和方向是( )| A. | 大小为3F,方向与5F方向相同 | B. | 大小为3F,方向与6F方向相同 | ||
| C. | 大小为6F,方向与5F方向相同 | D. | 大小为6F,方向与6F方向相同 |
12.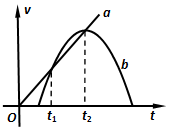 在同一条平直公路上行驶的a车和b车,其速度-时间图象分别为图中直线a和曲线b,由图可知( )
在同一条平直公路上行驶的a车和b车,其速度-时间图象分别为图中直线a和曲线b,由图可知( )
 在同一条平直公路上行驶的a车和b车,其速度-时间图象分别为图中直线a和曲线b,由图可知( )
在同一条平直公路上行驶的a车和b车,其速度-时间图象分别为图中直线a和曲线b,由图可知( )| A. | a车与b车一定相遇两次 | |
| B. | 在t2时刻b车的运动方向发生改变 | |
| C. | t1到t2时间内某时刻两车的加速度可能相同 | |
| D. | t1到t2时间内b车会追上并超越a车 |
2.一列简谐横波沿x轴正方向传播,t=0时波形图如图中实线所示,此时波刚好传到c点,t=0.6s时波恰好传到e点,波形如图中虚线所示,a、b、c、d、e是介质中的质点,下列说法正确的是( )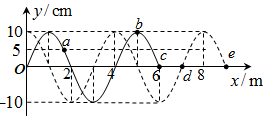
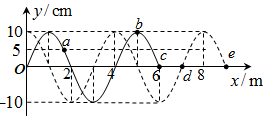
| A. | 当t=0.5s时质点b和质点c的位移相等 | |
| B. | 当t=0.6s时质点a的位移为-$5\sqrt{3}$cm | |
| C. | 质点c在0~0.6s时间内沿x轴正方向移动了3m | |
| D. | 质点d在0~0.6s时间内通过的路程为20cm | |
| E. | 这列简谐横波遇到频率为1Hz的另一列简谐横波时我们能够观察到干涉现象 |
9.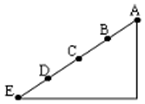 如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止释放,下列结论中正确的是( )
如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止释放,下列结论中正确的是( )
 如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止释放,下列结论中正确的是( )
如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止释放,下列结论中正确的是( )| A. | 物体到达各点的速率vB:vC:vD:vE=1:2:3:4 | |
| B. | 物体到达各点经历的时间tE=2tB=$\sqrt{2}$tc=$\frac{2}{\sqrt{3}}$tD | |
| C. | 物体从A 运动到E全过程的平均速度等于B点的瞬时速度 | |
| D. | 物体通过每一部分时,其速度增量vB-vA=vC-vB=vD-vC=vE-vD |
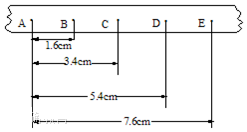 在研究匀变速直线运动规律的实验中,小车拖着纸带运动,每秒50次的打点计时器打出的纸带如图所示,选A、B、C、D、E共5个记数点,每相邻两点间还有4个实验点(图中未画出),以A为起点量出的到各点的位移,也标在图上:则B点的瞬时速度vB=0.17m/s,小车的加速度a=0.2m/s2.
在研究匀变速直线运动规律的实验中,小车拖着纸带运动,每秒50次的打点计时器打出的纸带如图所示,选A、B、C、D、E共5个记数点,每相邻两点间还有4个实验点(图中未画出),以A为起点量出的到各点的位移,也标在图上:则B点的瞬时速度vB=0.17m/s,小车的加速度a=0.2m/s2. 如图所示,一根弹簧上端固定在天花板上,下端连接质量为2kg的小球,静止时,弹簧伸长6cm,现对小球施加10N竖直向下F=10N拉力,重新静止后弹簧又伸长多少cm.(g=10m/s2弹簧在弹性限度内)
如图所示,一根弹簧上端固定在天花板上,下端连接质量为2kg的小球,静止时,弹簧伸长6cm,现对小球施加10N竖直向下F=10N拉力,重新静止后弹簧又伸长多少cm.(g=10m/s2弹簧在弹性限度内)