题目内容
9.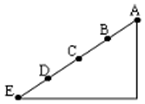 如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止释放,下列结论中正确的是( )
如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止释放,下列结论中正确的是( )| A. | 物体到达各点的速率vB:vC:vD:vE=1:2:3:4 | |
| B. | 物体到达各点经历的时间tE=2tB=$\sqrt{2}$tc=$\frac{2}{\sqrt{3}}$tD | |
| C. | 物体从A 运动到E全过程的平均速度等于B点的瞬时速度 | |
| D. | 物体通过每一部分时,其速度增量vB-vA=vC-vB=vD-vC=vE-vD |
分析 物体由A点静止释放后,物体做初速度为零的匀加速直线运动,且AB=BC=CD=DE,可直接应用初速度为零的匀加速直线运动通过连续相等的位移的推论.
解答 解:A、初速度为零的匀加速直线运动通过连续相等的位移所用的时间之比为,$1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}):(\sqrt{4}-\sqrt{3})$,${t}_{B}^{\;}:{t}_{B}^{\;}:{t}_{D}^{\;}:{t}_{E}^{\;}=1:\sqrt{2}:\sqrt{3}:\sqrt{4}$,又v=at,故物体到达各点的速率${v}_{B}^{\;}:{v}_{C}^{\;}:{v}_{D}^{\;}:{v}_{E}^{\;}=1:\sqrt{2}:\sqrt{3}:\sqrt{4}$,故A错误;
B、由A选项的推论,${t}_{B}^{\;}:{t}_{C}^{\;}:{t}_{D}^{\;}:{t}_{E}^{\;}=1:\sqrt{2}:\sqrt{3}:\sqrt{4}$可得,tE=2tB=$\sqrt{2}$tc=$\frac{2}{\sqrt{3}}{t}_{D}^{\;}$,故B正确;
C、由A选项的结论可得,B点是全程的中间时刻,故从A到E的全过程平均速度$\overline{v}={v}_{B}^{\;}$,故C正确;
D、由A选项的结论可得,△t不是定值,即速度变化量△v=at不是定值,故速度增量${v}_{B}^{\;}-{v}_{A}^{\;}≠{v}_{C}^{\;}-{v}_{B}^{\;}≠{v}_{D}^{\;}-{v}_{C}^{\;}≠{v}_{E}^{\;}-{v}_{D}^{\;}$,故D错误;
故选:BC
点评 熟练记忆匀变速直线运动的规律及其推论,遇到相应的题目要能做到熟练的应用.

 阅读快车系列答案
阅读快车系列答案| A. | 不带电的物体一定没有电荷 | |
| B. | 摩擦起电过程本质上是电荷从一个物体转移到另一个物体的过程 | |
| C. | 一根带电的导体棒放在潮湿的房间,发现导体棒不带电了,这过程中电荷不守恒 | |
| D. | 物体的带电荷量可以是任意值 |
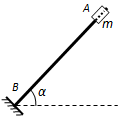 如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆上各处与滑块之间的动摩擦因素保持不变,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,滑块与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,下列说法中正确的是( )
如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆上各处与滑块之间的动摩擦因素保持不变,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,滑块与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,下列说法中正确的是( )| A. | 可以求出滑块下滑和上滑过程加速度的大小a1、a2 | |
| B. | 取过B点的水平面为零势能面,则可以判断滑块从A下滑至B的过程中,重力势能等于动能的位置在AB中点的下方 | |
| C. | 可以求出滑块在杆上运动的总路程S | |
| D. | 可以求出滑块第一次与挡板碰撞时重力做功的瞬时功率P |
 小车拉动纸带,打点计时器在甲、乙、丙、丁四条纸带上打下了如图所示的点迹,每条纸带的左端是与小车相连的,则下列叙述正确的是( )
小车拉动纸带,打点计时器在甲、乙、丙、丁四条纸带上打下了如图所示的点迹,每条纸带的左端是与小车相连的,则下列叙述正确的是( )| A. | 纸带甲打点均匀,表示小车的速度一定 | |
| B. | 纸带乙显示的平均速度最小 | |
| C. | 纸带丙表示小车的速度越来越小 | |
| D. | 纸带丁表示小车的速度越来越大 |

| A. | 甲在整个t=6 s时间内往返运动,平均速度为零 | |
| B. | 乙在整个t=6 s时间内往返运动,平均速度为零 | |
| C. | 甲在整个t=6 s时间内运动方向一直不变,它通过的总位移大小为4 m | |
| D. | 乙在整个t=6 s时间内运动方向一直不变,它通过的总位移大小为4 m |

(1)实验室提供了以下器材:打点计时器、一端附有滑轮的长木板、小车、纸带、细绳、钩码、刻度尺、导线、交流电源、复写纸、弹簧测力计.其中在本实验中不需要的器材是弹簧测力计.
(2)如图1所示,是某同学由打点计时器得到的表示小车运动过程的一条清晰纸带,纸带上两相邻计数点间还有四个点没有画出,打点计时器打点的时间间隔T=0.02s,其中x1=7.05cm、x2=7.68cm、x3=8.33cm、x4=8.95cm、x5=9.61cm、x6=10.26cm.下表列出了打点计时器打下B、C、F时小车的瞬时速度,请在表中填入打点计时器打下D、E两点时小车的瞬时速度.
| 位置 | B | C | D | E | F |
| 速度(m/s) | 0.737 | 0.801 | 0.994 |
(4)以A点为计时起点,在坐标图2中画出小车的速度-时间关系图线.
(5)根据你画出的小车的速度-时间关系图线计算出的小车的加速度a=0.65 m/s2.
 如图所示为某工厂的货物传送装置,水平运输带与一斜面MP平滑连接,小物体在此处无碰撞能量损失,小物体与运输带间的动摩擦因数为μ1=0.5,运输带运行的速度为v0=5m/s.在运输带上的N点将一小物体轻轻地放在上面,N点距运输带的右端距离为x=3m,小物体的质量为m=0.4kg.设小物体到达斜面最高点P时速度恰好为零,斜面长度L=1.25m,它与运输带的夹角为θ=37°.( sin37°=0.6,cos37°=0.8,g=10m/s2,空气阻力不计).求:
如图所示为某工厂的货物传送装置,水平运输带与一斜面MP平滑连接,小物体在此处无碰撞能量损失,小物体与运输带间的动摩擦因数为μ1=0.5,运输带运行的速度为v0=5m/s.在运输带上的N点将一小物体轻轻地放在上面,N点距运输带的右端距离为x=3m,小物体的质量为m=0.4kg.设小物体到达斜面最高点P时速度恰好为零,斜面长度L=1.25m,它与运输带的夹角为θ=37°.( sin37°=0.6,cos37°=0.8,g=10m/s2,空气阻力不计).求: