题目内容
7.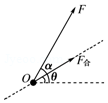 某科研单位设计了一空间飞行器,飞行器从地面静止起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰好与水平方向成θ=30°角的直线斜向右上方匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
某科研单位设计了一空间飞行器,飞行器从地面静止起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰好与水平方向成θ=30°角的直线斜向右上方匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )| A. | 加速时加速度的大小为g | B. | 加速时动力的大小等于mg | ||
| C. | 减速时动力的大小$\frac{1}{2}$mg | D. | 减速飞行时间2t后速度为零 |
分析 起飞时,飞行器受推力和重力,两力的合力与水平方向成30°角斜向上,根据几何关系求出合力,由牛顿第二定律求出加速度,根据匀加速运动速度公式求解最大速度;推力方向逆时针旋转60°后,先根据牛顿第二定律求解加速度,再求出继续上升的时间.
解答 解:A、B、起飞时,飞行器受推力和重力,两力的合力与水平方向成30°角斜向上,设动力为F,合力为Fb,如左图所示: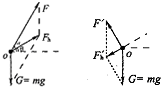
在△OFFb中,由几何关系得:F=$\sqrt{3}mg$,Fb=mg
由牛顿第二定律得飞行器的加速度为:a1=g
故A正确,B错误;
C、D、t时刻的速率:v=a1t=gt
推力方向逆时针旋转60°,合力的方向与水平方向成30°斜向下,推力F'跟合力F'h垂直,如图所示,
此时合力大小为:
F'h=mgsin30°
动力大小:
$F′=\frac{\sqrt{3}}{2}mg$
飞行器的加速度大小为:
a2=$\frac{mgsin30°}{m}$=$\frac{1}{2}$g
到最高点速度为零的时间为:t′=$\frac{v}{{a}_{2}}$=$\frac{gt}{\frac{1}{2}g}$=2t
故C错误,D正确;
故选:AD
点评 本题主要考查了牛顿第二定律及运动学基本公式的应用,要求同学们能正确对分析器进行受力分析并能结合几何关系求解,难度适中.

练习册系列答案
相关题目
18.在“探究小车速度随时间变化的规律”的实验中,如图1所示为一条记录小车运动情况的纸带,舍掉开头比较密集的点迹,在后面便于测量的地方找一个点做计时起点0,后面每隔4个点取一个计数点,交流电的频率为50HZ.

(1)在实验中,使用打点计时器操作步骤应先接通电源再释放小车(填“释放小车”或“接通电源”);
(2)试根据所提供的纸带,每隔0.10s测一次速度,算出包含各计数点0、1、2…附近各段的平均速度$\frac{△x}{△t}$,把它当作打点计时器打下这些点时小车的瞬时速度,并将各个速度值填入下表,请计算还未算好的速度并填入表格:
(3)以速度v为纵轴,时间t为横轴,建立直角坐标系,根据表中的数据,在坐标系中描点,并画出小车运动的v-t图象(已描好5个点).


(1)在实验中,使用打点计时器操作步骤应先接通电源再释放小车(填“释放小车”或“接通电源”);
(2)试根据所提供的纸带,每隔0.10s测一次速度,算出包含各计数点0、1、2…附近各段的平均速度$\frac{△x}{△t}$,把它当作打点计时器打下这些点时小车的瞬时速度,并将各个速度值填入下表,请计算还未算好的速度并填入表格:
| 计数点编号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 对应时刻t/s | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| 各计数点的速度v/(m•s-1) | 0.26 | 0.78 | 1.05 | 1.55 | 1.82 |

15.在“探究加速度与力、质量的关系”的实验时:
(1)我们已经知道,物体的加速度(a)同时跟合外力(F)和质量(m)两个因素有关.要研究这三个物理量之间的定量关系的基本思路是控制m一定,a与F关系;控制F,研究a与m的关系;.

(2)某同学的实验方案如图1所示,她想用砂和砂桶的重力表示小车受到的合外力,为了减少这种做法而带来的实验误差,你认为在实验中还应该采取的两项措施是:
a.平衡摩擦力;
b.砂和砂桶的质量远小于小车的质.
(3)该同学利用实验中打出的纸带求加速度时,处理方案有两种:
A、利用公式a=$\frac{2s}{{t}^{2}}$计算;B、根据a=$\frac{△s}{{T}^{2}}$利用逐差法计算.
两种方案中,你认为选择方案B比较合理.
(4)该同学平衡摩擦力后,将5个相同的砝码都放在小车上.挂上砝码盘,然后每次从小车上取一个砝码添加到砝码盘中,测量小车的加速度.小车的加速度a与砝码盘中砝码总重力F的实验数据如上表,请你根据表格中的数据在上面的坐标系中做出a-F图象;
(5)根据该同学提供的实验数据在图2中作出的a-F图线不通过原点,请说明主要原因:分析拉力时未计入砝码盘的重力.
(1)我们已经知道,物体的加速度(a)同时跟合外力(F)和质量(m)两个因素有关.要研究这三个物理量之间的定量关系的基本思路是控制m一定,a与F关系;控制F,研究a与m的关系;.

(2)某同学的实验方案如图1所示,她想用砂和砂桶的重力表示小车受到的合外力,为了减少这种做法而带来的实验误差,你认为在实验中还应该采取的两项措施是:
a.平衡摩擦力;
b.砂和砂桶的质量远小于小车的质.
(3)该同学利用实验中打出的纸带求加速度时,处理方案有两种:
A、利用公式a=$\frac{2s}{{t}^{2}}$计算;B、根据a=$\frac{△s}{{T}^{2}}$利用逐差法计算.
两种方案中,你认为选择方案B比较合理.
| 砂和砂桶总重力F(N) | 0.196 | 0.392 | 0.588 | 0.784 | 0.980 |
| 加速度a(m•s-2) | 0.69 | 1.18 | 1.66 | 2.18 | 2.70 |
(5)根据该同学提供的实验数据在图2中作出的a-F图线不通过原点,请说明主要原因:分析拉力时未计入砝码盘的重力.
2. 图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动.当振子位于A点时弹簧处于自然伸长状态,取竖直向上的方向为正方向,振子的质量为m,重力加速度为g,振子的位移x随时间的变化如图乙所示.下列说法正确的是( )
图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动.当振子位于A点时弹簧处于自然伸长状态,取竖直向上的方向为正方向,振子的质量为m,重力加速度为g,振子的位移x随时间的变化如图乙所示.下列说法正确的是( )
 图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动.当振子位于A点时弹簧处于自然伸长状态,取竖直向上的方向为正方向,振子的质量为m,重力加速度为g,振子的位移x随时间的变化如图乙所示.下列说法正确的是( )
图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动.当振子位于A点时弹簧处于自然伸长状态,取竖直向上的方向为正方向,振子的质量为m,重力加速度为g,振子的位移x随时间的变化如图乙所示.下列说法正确的是( )| A. | t=0.8s时,振子的速度方向竖直向下 | |
| B. | t=0.6s和t=1.0s时,振子的速度相同 | |
| C. | t=0.4s和t=1.2s时,振子的加速度相同 | |
| D. | t=1.4s时,振子位于O点下方6cm处 | |
| E. | t=1.2s到t=1.6s的时间内,振子的速度逐渐变大 |
12.质点做直线运动的位置x与时间t的关系式为x=5t+t2+3(各物理量均采用国际单位制),则该质点( )
| A. | 第1s内位移为9m | B. | 前两秒内的平均速度为6m/s | ||
| C. | 质点的加速度为1m/s2 | D. | 任意1s内的速度增量都是2m/s |
19.对物体带电现象的叙述,正确的是( )
| A. | 不带电的物体一定没有电荷 | |
| B. | 摩擦起电过程本质上是电荷从一个物体转移到另一个物体的过程 | |
| C. | 一根带电的导体棒放在潮湿的房间,发现导体棒不带电了,这过程中电荷不守恒 | |
| D. | 物体的带电荷量可以是任意值 |
17.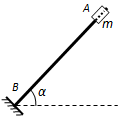 如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆上各处与滑块之间的动摩擦因素保持不变,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,滑块与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,下列说法中正确的是( )
如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆上各处与滑块之间的动摩擦因素保持不变,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,滑块与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,下列说法中正确的是( )
 如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆上各处与滑块之间的动摩擦因素保持不变,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,滑块与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,下列说法中正确的是( )
如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆上各处与滑块之间的动摩擦因素保持不变,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,滑块与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,下列说法中正确的是( )| A. | 可以求出滑块下滑和上滑过程加速度的大小a1、a2 | |
| B. | 取过B点的水平面为零势能面,则可以判断滑块从A下滑至B的过程中,重力势能等于动能的位置在AB中点的下方 | |
| C. | 可以求出滑块在杆上运动的总路程S | |
| D. | 可以求出滑块第一次与挡板碰撞时重力做功的瞬时功率P |

