题目内容
2.一列简谐横波沿x轴正方向传播,t=0时波形图如图中实线所示,此时波刚好传到c点,t=0.6s时波恰好传到e点,波形如图中虚线所示,a、b、c、d、e是介质中的质点,下列说法正确的是( )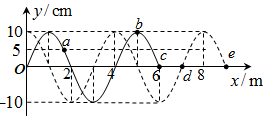
| A. | 当t=0.5s时质点b和质点c的位移相等 | |
| B. | 当t=0.6s时质点a的位移为-$5\sqrt{3}$cm | |
| C. | 质点c在0~0.6s时间内沿x轴正方向移动了3m | |
| D. | 质点d在0~0.6s时间内通过的路程为20cm | |
| E. | 这列简谐横波遇到频率为1Hz的另一列简谐横波时我们能够观察到干涉现象 |
分析 由图可知波的波长,而由两列波的波形图可得两波形相距的时间与周期的关系,则可得出波速的表达式;由波速可知周期的表达式,则可得出质点的路程及位移,两列波发生干涉它们的频率必须相同
解答 解:由题意可得该波向右传播,起振的方向向上,波长是4m,0.6s的时间内传播的距离是$\frac{3}{4}λ$,所以波的周期T=0.6×$\frac{4}{3}$=0.8s,$f=\frac{1}{T}=\frac{1}{0.8}=\frac{5}{4}Hz$,$ω=2πf=\frac{5π}{2}$
A、该波是方程:$y=Asin[2π(\frac{t}{T}-\frac{x}{λ})]$当t=0.5s时质点b的位移:
${y}_{b}^{\;}=0.10×sin[2π(\frac{0.5}{0.8}-\frac{5}{4})]=-\frac{\sqrt{2}}{20}m$
c点的位移:
${y}_{c}^{\;}=0.10×sin[2π(\frac{0.5}{0.8}-\frac{6}{4})]=-\frac{\sqrt{2}}{20}m$,当质点b、c的位移相同.故A正确;
B、质点a的初相为$\frac{π}{6}$,振动方程$y=Asin(ωt+φ)=10sin(\frac{5π}{2}t+\frac{π}{6})$,当t=0.6s时$y=10sin(\frac{5}{2}π×0.6+\frac{π}{6})=-5\sqrt{3}cm$,故B正确;
C、质点c在这段时间内只是沿振动的方向振动,没有沿x轴正方向移动.故C错误.
D、由图可知,质点d在0.6s内先向上运动到达最高点后又返回平衡位置,在这段时间内通过的路程是2倍的振幅,为20cm.故D正确.
E、因为发生干涉的两列波频率相同,这列简谐横波的频率为$\frac{5}{4}Hz$,遇到频率为1Hz的另一列简谐横波时,我们不能够观察到干涉现象,故E错误;
故选:ABD
点评 本题考查对波动图象的理解能力.知道两个时刻的波形时,往往应用波形的平移法来理解.该题中的A选项使用波的方程是该题的难点,也可以使用作图的方法来解决.

 阅读快车系列答案
阅读快车系列答案| A. | 第1s内位移为9m | B. | 前两秒内的平均速度为6m/s | ||
| C. | 质点的加速度为1m/s2 | D. | 任意1s内的速度增量都是2m/s |
 如图所示,在竖直平面内固定有两个很靠近的共面同心圆轨道,外圆光滑,内圆粗糙.一质量为m的小球从轨道的最低点以初速度v0向右运动,球的直径略小于两圆间距,球运动的轨道半径为R,不计空气阻力.设小球过最低点时重力势能为零,已知重力加速度为g,下列说法正确的是( )
如图所示,在竖直平面内固定有两个很靠近的共面同心圆轨道,外圆光滑,内圆粗糙.一质量为m的小球从轨道的最低点以初速度v0向右运动,球的直径略小于两圆间距,球运动的轨道半径为R,不计空气阻力.设小球过最低点时重力势能为零,已知重力加速度为g,下列说法正确的是( )| A. | 若小球运动到最高点时速度为0,则小球机械能守恒 | |
| B. | 若经过足够长时间,小球最终的机械能可能为mgR | |
| C. | 若使小球始终做完整的圆周运动,则v0可以小于$\sqrt{5gR}$ | |
| D. | 若小球第一次运动到最高点时速度大小为0,则v0等于$\sqrt{4gR}$ |
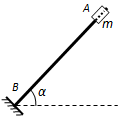 如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆上各处与滑块之间的动摩擦因素保持不变,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,滑块与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,下列说法中正确的是( )
如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆上各处与滑块之间的动摩擦因素保持不变,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,滑块与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,下列说法中正确的是( )| A. | 可以求出滑块下滑和上滑过程加速度的大小a1、a2 | |
| B. | 取过B点的水平面为零势能面,则可以判断滑块从A下滑至B的过程中,重力势能等于动能的位置在AB中点的下方 | |
| C. | 可以求出滑块在杆上运动的总路程S | |
| D. | 可以求出滑块第一次与挡板碰撞时重力做功的瞬时功率P |
 一根大弹簧内套一根小弹簧,大弹簧比小弹簧长0.20m,它们的下端固定在地面上,上端自由,如图甲所示.当加力压缩此组合弹簧时,测得力和弹簧压缩距离之间的关系如图乙所示,则两根弹簧的劲度系数分别是(设大弹簧劲度系数为k1,小弹簧劲度系数为k2)( )
一根大弹簧内套一根小弹簧,大弹簧比小弹簧长0.20m,它们的下端固定在地面上,上端自由,如图甲所示.当加力压缩此组合弹簧时,测得力和弹簧压缩距离之间的关系如图乙所示,则两根弹簧的劲度系数分别是(设大弹簧劲度系数为k1,小弹簧劲度系数为k2)( )| A. | k1=100 N/m,k2=200 N/m | B. | k1=200 N/m,k2=100 N/m | ||
| C. | k1=100 N/m,k2=300 N/m | D. | k1=300 N/m,k2=200 N/m |
 小车拉动纸带,打点计时器在甲、乙、丙、丁四条纸带上打下了如图所示的点迹,每条纸带的左端是与小车相连的,则下列叙述正确的是( )
小车拉动纸带,打点计时器在甲、乙、丙、丁四条纸带上打下了如图所示的点迹,每条纸带的左端是与小车相连的,则下列叙述正确的是( )| A. | 纸带甲打点均匀,表示小车的速度一定 | |
| B. | 纸带乙显示的平均速度最小 | |
| C. | 纸带丙表示小车的速度越来越小 | |
| D. | 纸带丁表示小车的速度越来越大 |
 如图所示的电路中,电源的电动势E和内阻r一定,A、B为平行板电容器的两块正对金属板,R1为光敏电阻(光照越强电阻越小).当R2的滑动触头P在a端时,闭合开关S,此时电流表A和电压表V的示数分别为I和U.以下说法正确的是( )
如图所示的电路中,电源的电动势E和内阻r一定,A、B为平行板电容器的两块正对金属板,R1为光敏电阻(光照越强电阻越小).当R2的滑动触头P在a端时,闭合开关S,此时电流表A和电压表V的示数分别为I和U.以下说法正确的是( )| A. | 若仅将R2的滑动触头P向b端移动,则I不变,U增大 | |
| B. | 若仅增大A、B板间距离,则电容器所带电荷量减少 | |
| C. | 若仅用更强的光照射,则I增大,U增大,电容器所带电荷量增加 | |
| D. | 若仅增大A、B板间距离,则悬挂小球的细绳与竖直方向的夹角减小 |
| A. | 质点初速度0 | B. | 质点初速度5m/s | ||
| C. | 质点加速度10m/s2 | D. | 质点加速度5m/s2 |