题目内容
5. 如图,一质量为M=1kg的光滑大圆环,用一细轻杆固定在竖直平面内;套在大环上质量为m=0.2kg的小环(可视为质点),从大环的最高处由静止滑下.重力加速度大小为g.当小环滑到大环的最低点时,大环对轻杆拉力的大小为( )
如图,一质量为M=1kg的光滑大圆环,用一细轻杆固定在竖直平面内;套在大环上质量为m=0.2kg的小环(可视为质点),从大环的最高处由静止滑下.重力加速度大小为g.当小环滑到大环的最低点时,大环对轻杆拉力的大小为( )| A. | 10N | B. | 20N | C. | 30N | D. | 40N |
分析 根据牛顿第二定律求出小环运动到最低点时,大环对它的拉力,再用隔离法对大环分析,求出大环对轻杆的拉力大小.
解答 解:小环在最低点时,根据牛顿第二定律得:
F-mg=m$\frac{{v}^{2}}{R}$,
得:F=mg+m$\frac{{v}^{2}}{R}$,
小环从最高到最低,由机械能守恒定律,则有:
$\frac{1}{2}m{v^2}=mg•2R$;
对大环分析,有:
T=F+Mg=m(g+$\frac{{v}^{2}}{R}$)+Mg=5mg+Mg=5×0.2×10+1×10=20N.
故选:B.
点评 解决本题的关键搞清小环做圆周运动向心力的来源,运用牛顿第二定律进行求解,不难.

练习册系列答案
相关题目
15.近年来,我市电力供应紧张,节约用电尤为重要,下列属于节约用电措施的是( )
| A. | 电视机不用时切断电源 | B. | 离开教室时随手关灯 | ||
| C. | 夏天用空调时,把温度调得很低 | D. | 尽量少开启电冰箱门 |
16. 如图所示,空间存在着与圆台母线垂直向外的磁场,各处的磁感应强度大小均为B=0.5T,圆台母线与竖直方向的夹角为θ=37°,一个质量为m=0.8kg、周长为L=3m的匀质金属环位于圆台底部.给圆环通以恒定的电流I=8A后,圆环由静止向上做匀加速直线运动,经过时间t=2s后撤去该恒定电流并保持圆环闭合,圆环全程上升的最大高度为H.重力加速度为g=10m/s2,磁场的范围足够大.在圆环向上运动的过程中,下列说法正确的是(已知:sin37°=0.6,cos37°=0.8)( )
如图所示,空间存在着与圆台母线垂直向外的磁场,各处的磁感应强度大小均为B=0.5T,圆台母线与竖直方向的夹角为θ=37°,一个质量为m=0.8kg、周长为L=3m的匀质金属环位于圆台底部.给圆环通以恒定的电流I=8A后,圆环由静止向上做匀加速直线运动,经过时间t=2s后撤去该恒定电流并保持圆环闭合,圆环全程上升的最大高度为H.重力加速度为g=10m/s2,磁场的范围足够大.在圆环向上运动的过程中,下列说法正确的是(已知:sin37°=0.6,cos37°=0.8)( )
 如图所示,空间存在着与圆台母线垂直向外的磁场,各处的磁感应强度大小均为B=0.5T,圆台母线与竖直方向的夹角为θ=37°,一个质量为m=0.8kg、周长为L=3m的匀质金属环位于圆台底部.给圆环通以恒定的电流I=8A后,圆环由静止向上做匀加速直线运动,经过时间t=2s后撤去该恒定电流并保持圆环闭合,圆环全程上升的最大高度为H.重力加速度为g=10m/s2,磁场的范围足够大.在圆环向上运动的过程中,下列说法正确的是(已知:sin37°=0.6,cos37°=0.8)( )
如图所示,空间存在着与圆台母线垂直向外的磁场,各处的磁感应强度大小均为B=0.5T,圆台母线与竖直方向的夹角为θ=37°,一个质量为m=0.8kg、周长为L=3m的匀质金属环位于圆台底部.给圆环通以恒定的电流I=8A后,圆环由静止向上做匀加速直线运动,经过时间t=2s后撤去该恒定电流并保持圆环闭合,圆环全程上升的最大高度为H.重力加速度为g=10m/s2,磁场的范围足够大.在圆环向上运动的过程中,下列说法正确的是(已知:sin37°=0.6,cos37°=0.8)( )| A. | 圆环的最大速度为10m/s | B. | 圆环产生的最大电动势为6V | ||
| C. | 圆环上升过程中安培力做功32J | D. | 圆环先有收缩后有扩张的趋势 |
20.宇宙飞船在半径为R1的轨道上运行,变轨后的半径为R2,R1>R2.宇宙飞船绕地球做匀速圆周运动,则变轨后宇宙飞船的( )
| A. | 线速度变小 | B. | 角速度变大 | C. | 周期变大 | D. | 向心加速度变小 |
17. 如图所示,x轴在水平地面上,y轴沿竖直方向.图中画出了从y轴上不同位置沿x轴正向水平抛出的三个小球a、b和c的运动轨迹.小球a从(0,2L)抛出,落在(2L,0)处;小球b、c从(0,L)抛出,分别落在(2L,0)和(L,0)处.不计空气阻力,下列说法正确的是( )
如图所示,x轴在水平地面上,y轴沿竖直方向.图中画出了从y轴上不同位置沿x轴正向水平抛出的三个小球a、b和c的运动轨迹.小球a从(0,2L)抛出,落在(2L,0)处;小球b、c从(0,L)抛出,分别落在(2L,0)和(L,0)处.不计空气阻力,下列说法正确的是( )
 如图所示,x轴在水平地面上,y轴沿竖直方向.图中画出了从y轴上不同位置沿x轴正向水平抛出的三个小球a、b和c的运动轨迹.小球a从(0,2L)抛出,落在(2L,0)处;小球b、c从(0,L)抛出,分别落在(2L,0)和(L,0)处.不计空气阻力,下列说法正确的是( )
如图所示,x轴在水平地面上,y轴沿竖直方向.图中画出了从y轴上不同位置沿x轴正向水平抛出的三个小球a、b和c的运动轨迹.小球a从(0,2L)抛出,落在(2L,0)处;小球b、c从(0,L)抛出,分别落在(2L,0)和(L,0)处.不计空气阻力,下列说法正确的是( )| A. | b和c运动时间相同 | B. | a和b初速度相同 | ||
| C. | a的运动时间是b的两倍 | D. | b的初速度是c的两倍 |
14.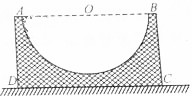 某大型游乐场内的新型滑行运动可以等效为如图所示的物理模型.大型矩形台内有半圆柱形凹槽.一个小朋友在A点由静止开始滑人凹槽内.不计滑板与圆形凹槽间的摩擦,滑到另一端B处恰好静止,整个过程中矩形台保持静止状态.则该小朋友从A点滑至B端的过程中( )
某大型游乐场内的新型滑行运动可以等效为如图所示的物理模型.大型矩形台内有半圆柱形凹槽.一个小朋友在A点由静止开始滑人凹槽内.不计滑板与圆形凹槽间的摩擦,滑到另一端B处恰好静止,整个过程中矩形台保持静止状态.则该小朋友从A点滑至B端的过程中( )
 某大型游乐场内的新型滑行运动可以等效为如图所示的物理模型.大型矩形台内有半圆柱形凹槽.一个小朋友在A点由静止开始滑人凹槽内.不计滑板与圆形凹槽间的摩擦,滑到另一端B处恰好静止,整个过程中矩形台保持静止状态.则该小朋友从A点滑至B端的过程中( )
某大型游乐场内的新型滑行运动可以等效为如图所示的物理模型.大型矩形台内有半圆柱形凹槽.一个小朋友在A点由静止开始滑人凹槽内.不计滑板与圆形凹槽间的摩擦,滑到另一端B处恰好静止,整个过程中矩形台保持静止状态.则该小朋友从A点滑至B端的过程中( )| A. | 地面对矩形台的摩擦力方向先水平向左,后水平向右 | |
| B. | 地面对矩形台的摩擦力方向先水平向右,后水平向左 | |
| C. | 地面对矩形台的支持力的大小始终大于小朋友,滑板和滑梯的总重力的大小 | |
| D. | 地面对矩形台的支持力的大小先小于、后大于、再小于小朋友、滑板和矩形台总重力的大小 |
1.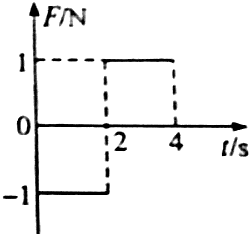 静止在光滑水平面上的物体,受到水平拉力F的作用,拉力F随时间t的变化如图所示,则( )
静止在光滑水平面上的物体,受到水平拉力F的作用,拉力F随时间t的变化如图所示,则( )
 静止在光滑水平面上的物体,受到水平拉力F的作用,拉力F随时间t的变化如图所示,则( )
静止在光滑水平面上的物体,受到水平拉力F的作用,拉力F随时间t的变化如图所示,则( )| A. | 4s内物体的位移为零 | B. | 4s内拉力对物体做功不为零 | ||
| C. | 4s末物体的速度为零 | D. | 4s内拉力对物体冲量为零 |
 在“用单摆测定重力加速度”的实验中:
在“用单摆测定重力加速度”的实验中: 如图所示,士兵射击训练时,射击枪水平放置,射击枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶之间的距离s=100m,子弹射出的水平速度v=250m/s,子弹从枪口射出的瞬 间目标靶由静止开始释放,不计空气阻力,取重力加速度g为10m/s2,求:
如图所示,士兵射击训练时,射击枪水平放置,射击枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶之间的距离s=100m,子弹射出的水平速度v=250m/s,子弹从枪口射出的瞬 间目标靶由静止开始释放,不计空气阻力,取重力加速度g为10m/s2,求: