题目内容
20.利用所学物理知识解答下列问题:
(1)“研究平抛物体的运动”实验的装置如图1所示,在实验前应调节将斜槽直至末端切线水平,实验时保证小球每次必须从斜面上的同一位置由静止开始释放.
(2)某次实验记录由于没有记录抛出点,数据处理时选择A点为坐标原点(0,0),结合实验中重锤的情况确定坐标系,如图2中背景方格的边长均为0.05m,取g=l0m/s2,小球运动中水平分速度的大小是1.5m/s,小球经过B点时的速度大小是2.5m/s,小球平抛运动抛出点的x轴坐标为-0.2m.
分析 在实验中让小球能做平抛运动,并能描绘出运动轨迹,实验成功的关键是小球是否初速度水平,要求从同一位置多次无初速度释放,这样才能确保每次平抛轨迹相同;
在竖直方向上,根据连续相等时间内的位移之差是一恒量求出相等的时间间隔,即A到B的时间,结合水平位移和时间求出初速度.
根据某段时间内的平均速度等于中间时刻的瞬时速度求出B点的竖直分速度,结合平行四边形定则求出B点的速度.
根据速度时间公式求出抛出点到B点的时间,从而求出B点与抛出点的水平位移和竖直位移,得出抛出点的坐标.
解答 解:(1)实验中必须保证小球做平抛运动,而平抛运动要求有水平初速度且只受重力作用;
由于要记录小球的运动轨迹,必须重复多次,才能画出几个点,因此为了保证每次平抛的轨迹相同,所以要求小球每次从同一高度释放.
(2)根据△y=2L=gT2得:T=$\sqrt{\frac{2×0.05}{10}}$s=0.1s,则A运动到B的时间为0.1s.
平抛运动的初速度为:v0=$\frac{x}{T}$=$\frac{3×0.05}{0.1}$=1.5m/s.
B点竖直分速度为:vyB=$\frac{{y}_{AC}}{2T}$=$\frac{8×0.05}{2×0.1}$=2m/s,
则B点的速度为:vB=$\sqrt{{v}_{0}^{2}+{v}_{yB}^{2}}$=$\sqrt{1.{5}^{2}+{2}^{2}}$=2.5m/s.
抛出点到B点的时间为:t=$\frac{{v}_{yB}}{g}$=$\frac{2}{10}$s=0.2s,
则x=0.1-v0t=0.1-1.5×0.2=-0.2m,
故答案为:(1)水平,同一位置;(2)1.5,2.5,-0.2.
点评 对于平抛运动问题,一定明确其水平和竖直方向运动特点,尤其是在竖直方向熟练应用匀变速直线运动的规律和推论解题.

 名校课堂系列答案
名校课堂系列答案 如图所示,两根直木棍AB和CD相互平行,斜靠在竖直墙壁上固定不动,一个圆筒从木棍的上部以初速度v0匀速滑下;若保持两木棍倾角不变,将两棍间的距离减小后固定不动,仍将圆筒放在两木棍上部以初速度v0滑下,下列判断正确的是( )
如图所示,两根直木棍AB和CD相互平行,斜靠在竖直墙壁上固定不动,一个圆筒从木棍的上部以初速度v0匀速滑下;若保持两木棍倾角不变,将两棍间的距离减小后固定不动,仍将圆筒放在两木棍上部以初速度v0滑下,下列判断正确的是( )| A. | 仍匀速滑下 | B. | 匀加速下滑 | ||
| C. | 减速下滑 | D. | 以上三种运动均可能 |
 如图所示,两根足够长的平行金属导轨相距为L,其中NO1、QO2部分水平,倾斜部分MN、PQ与水平面的夹角均为α,整个空间存在磁感应强度为B的匀强磁场,磁场方向垂直导轨平面MNQP向上,长为L的金属棒ab、cd与导轨垂直放置且接触良好,其中ab光滑,cd粗糙,棒的质量均为m、电阻均为R.将ab由静止释放,在ab下滑至速度刚达到稳定的过程中,cd始终静止不动.若导轨电阻不计,重力加速度为g,则在上述过程中( )
如图所示,两根足够长的平行金属导轨相距为L,其中NO1、QO2部分水平,倾斜部分MN、PQ与水平面的夹角均为α,整个空间存在磁感应强度为B的匀强磁场,磁场方向垂直导轨平面MNQP向上,长为L的金属棒ab、cd与导轨垂直放置且接触良好,其中ab光滑,cd粗糙,棒的质量均为m、电阻均为R.将ab由静止释放,在ab下滑至速度刚达到稳定的过程中,cd始终静止不动.若导轨电阻不计,重力加速度为g,则在上述过程中( )| A. | ab棒做加速度减小的加速运动 | |
| B. | ab棒下滑的最大速度为$\frac{mgRsinα}{B^2L^2}$ | |
| C. | cd棒所受摩擦力的最大值为mgsinαcosα | |
| D. | cd棒中产生的热量等于ab棒机械能的减少量 |
 如图,“嫦娥三号”卫星要经过一系列的调控和变轨,才能最终顺利降落在月球表面.它先在地月转移轨道的P点调整后进入环月圆形轨道1,进一步调整后进入环月椭圆轨道2.有关“嫦娥三号”下列说法正确的是( )
如图,“嫦娥三号”卫星要经过一系列的调控和变轨,才能最终顺利降落在月球表面.它先在地月转移轨道的P点调整后进入环月圆形轨道1,进一步调整后进入环月椭圆轨道2.有关“嫦娥三号”下列说法正确的是( )| A. | 在地球上的发射速度一定大于第二宇宙速度 | |
| B. | 在P点由轨道1进入轨道2需要减速 | |
| C. | 在轨道2经过P点时速度大于Q点速度 | |
| D. | 分别由轨道1与轨道2经P点时,向心加速度相同 |
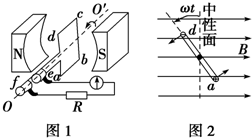 图1是交流发电机模型示意图.在磁感应强度为B的匀强磁场中,有一矩形线圈abcd可绕线圈平面内垂直于磁感线的轴OO′转动,由线圈引出的导线ae和df分别与两个跟线圈一起绕OO′转动的金属圆环相连接,金属圆环又分别与两个固定的电刷保持滑动接触,这样矩形线圈在转动中就可以保持和外电路电阻R形成闭合电路.图2是线圈的主视图,导线ab和cd分别用它们的横截面来表示.已知ab长度为L1,bc长度为L2,线圈以恒定角速度ω逆时针转动.(只考虑单匝线圈)
图1是交流发电机模型示意图.在磁感应强度为B的匀强磁场中,有一矩形线圈abcd可绕线圈平面内垂直于磁感线的轴OO′转动,由线圈引出的导线ae和df分别与两个跟线圈一起绕OO′转动的金属圆环相连接,金属圆环又分别与两个固定的电刷保持滑动接触,这样矩形线圈在转动中就可以保持和外电路电阻R形成闭合电路.图2是线圈的主视图,导线ab和cd分别用它们的横截面来表示.已知ab长度为L1,bc长度为L2,线圈以恒定角速度ω逆时针转动.(只考虑单匝线圈) 力大小.
力大小.
 如图,半径为R的水平圆盘正以中心O为转轴匀速转动,从圆板中心O的正上方h高处水平抛出一球,此时半径OB恰与球的初速度方向一致.要使球正好落在B点,已知重力加速度为g,求:
如图,半径为R的水平圆盘正以中心O为转轴匀速转动,从圆板中心O的正上方h高处水平抛出一球,此时半径OB恰与球的初速度方向一致.要使球正好落在B点,已知重力加速度为g,求: