题目内容
14.嫦娥五号探测器预计在2017年由长征五号运载火箭执行发射,全面完成探月工程绕月、落月、返回地球的总目标.已知地球半径为月球的3.7倍,地球表面的重力加速度约为月球表面重力加速度的6倍,已知地球的第一宇宙速度为7.9km/s,则月球的第一宇宙速度约为( )| A. | 0.36km/s | B. | 0.87km/s | C. | 1.32km/s | D. | 1.68km/s |
分析 卫星在近月轨道做匀速圆周运动时,重力提供向心力m卫g月=m卫$\frac{{v}_{月}^{2}}{{R}_{月}^{\;}}$,可解得近月卫星的运行速度,即为月球的第一宇宙速度.
解答 解:根据质量为m分别绕地球与月球表面做匀速圆周运动,
则有:m卫g地=m卫$\frac{{v}_{地}^{2}}{{R}_{地}}$,
m卫g月=m卫$\frac{{v}_{月}^{2}}{{R}_{月}^{\;}}$,
解得:v月=$\sqrt{\frac{{g}_{月}{R}_{地}}{{g}_{地}{R}_{月}}}$v地;
因地球的半径约为月球半径的3.7倍,地球表面的重力加速度约为月球表面重力加速度的6倍,
地球的第一宇宙速度约为7.9km/s.
则有:v月=1.68km/s,故ABC错误,D正确;
故选:D.
点评 本题是卫星类型问题,关键是要建立物理模型,运用万有引力定律和向心力知识,加上数学变换来求解.

练习册系列答案
相关题目
2. 如图所示,a、b是地球赤道上的两点,b、c是地球表面上不同纬度上的两点,若a、b、c三点随地球的自转都看作是匀速圆周运动,则下列说法中正确的是( )
如图所示,a、b是地球赤道上的两点,b、c是地球表面上不同纬度上的两点,若a、b、c三点随地球的自转都看作是匀速圆周运动,则下列说法中正确的是( )
 如图所示,a、b是地球赤道上的两点,b、c是地球表面上不同纬度上的两点,若a、b、c三点随地球的自转都看作是匀速圆周运动,则下列说法中正确的是( )
如图所示,a、b是地球赤道上的两点,b、c是地球表面上不同纬度上的两点,若a、b、c三点随地球的自转都看作是匀速圆周运动,则下列说法中正确的是( )| A. | a、b两点的角速度相同,而c点的角速度不同 | |
| B. | a、b两点的线速度大小相等 | |
| C. | b、c两点的线速度大小相等 | |
| D. | b、c两点的轨道半径相同 |
9.据报道在太阳系之外发现了一颗可能适合人类居住的类地行星Gliese581C,天文学观察发现绕该行星做圆周运动的卫星的轨道半径为月球绕地球做圆周运动半径的p倍,周期为月球绕地球做圆周运动周期的q倍.已知地球半径为R,表面重力加速度为g.万有引力常量为G,则该行星的质量为( )
| A. | $\frac{gR{p}^{2}}{G{p}^{3}}$ | B. | $\frac{g{R}^{2}{q}^{3}}{G{p}^{2}}$ | C. | $\frac{gR{q}^{2}}{G{p}^{3}}$ | D. | $\frac{g{R}^{2}{p}^{3}}{G{q}^{2}}$ |
19. 如图所示,斜面上放有两个完全相同的物体a、b,两物体间用一根细线连接,在细线的中点加一与斜面垂直的拉力F,使两物体均处于静止状态.下列说法正确的是( )
如图所示,斜面上放有两个完全相同的物体a、b,两物体间用一根细线连接,在细线的中点加一与斜面垂直的拉力F,使两物体均处于静止状态.下列说法正确的是( )
 如图所示,斜面上放有两个完全相同的物体a、b,两物体间用一根细线连接,在细线的中点加一与斜面垂直的拉力F,使两物体均处于静止状态.下列说法正确的是( )
如图所示,斜面上放有两个完全相同的物体a、b,两物体间用一根细线连接,在细线的中点加一与斜面垂直的拉力F,使两物体均处于静止状态.下列说法正确的是( )| A. | 物体a对斜面的压力大于物体b对斜面的压力 | |
| B. | a、b两物体受到的摩擦力的方向一定均沿斜面向上 | |
| C. | 物体b可能受到3个力作用,也可能受到4个力作用 | |
| D. | 当逐渐增大拉力F时,a、b物体可能同时开始滑动 |
6.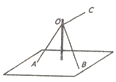 如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
 如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )| A. | 20$\sqrt{3}$N | B. | 40N | C. | 40$\sqrt{3}$N | D. | 60N |
3. 回旋加速器在核科学、核技术、核医学等高新技术领域得到了广泛应用,有力地推动了现代科学技术的发展.回旋加速器的原理如图所示,D1和D2是两个正对的中空半圆金属盒,它们的半径均为R,且分别接在电压一定的交流电源两端,可在两金属盒之间的狭缝处形成变化的加速电场,两金属盒处于与盒面垂直、磁感应强度为B的匀强磁场中,A点处的粒子源不断产生带电粒子,它们在两盒之间被电场加速后在金属盒内的磁场中做匀速圆周运动.调节交流电源的频率,使得每当带电粒子运动到现金金属盒之间的狭缝边缘时恰好改变加速电场的方向.从而保证带电粒子能在两金属盒之间狭缝处总被加速,且最终都能沿位于D2盒边缘的C口射出.该回旋加速器可将原来静止的α粒子(氦原子核)加速到最大速率v使它获得的最大动能为Ek.若带电粒子在A点的初速度、所受重力、通过狭缝的时间及C口的口径大小均可忽略不计,且不考虑相对论效应,则用该回旋加速器( )
回旋加速器在核科学、核技术、核医学等高新技术领域得到了广泛应用,有力地推动了现代科学技术的发展.回旋加速器的原理如图所示,D1和D2是两个正对的中空半圆金属盒,它们的半径均为R,且分别接在电压一定的交流电源两端,可在两金属盒之间的狭缝处形成变化的加速电场,两金属盒处于与盒面垂直、磁感应强度为B的匀强磁场中,A点处的粒子源不断产生带电粒子,它们在两盒之间被电场加速后在金属盒内的磁场中做匀速圆周运动.调节交流电源的频率,使得每当带电粒子运动到现金金属盒之间的狭缝边缘时恰好改变加速电场的方向.从而保证带电粒子能在两金属盒之间狭缝处总被加速,且最终都能沿位于D2盒边缘的C口射出.该回旋加速器可将原来静止的α粒子(氦原子核)加速到最大速率v使它获得的最大动能为Ek.若带电粒子在A点的初速度、所受重力、通过狭缝的时间及C口的口径大小均可忽略不计,且不考虑相对论效应,则用该回旋加速器( )
 回旋加速器在核科学、核技术、核医学等高新技术领域得到了广泛应用,有力地推动了现代科学技术的发展.回旋加速器的原理如图所示,D1和D2是两个正对的中空半圆金属盒,它们的半径均为R,且分别接在电压一定的交流电源两端,可在两金属盒之间的狭缝处形成变化的加速电场,两金属盒处于与盒面垂直、磁感应强度为B的匀强磁场中,A点处的粒子源不断产生带电粒子,它们在两盒之间被电场加速后在金属盒内的磁场中做匀速圆周运动.调节交流电源的频率,使得每当带电粒子运动到现金金属盒之间的狭缝边缘时恰好改变加速电场的方向.从而保证带电粒子能在两金属盒之间狭缝处总被加速,且最终都能沿位于D2盒边缘的C口射出.该回旋加速器可将原来静止的α粒子(氦原子核)加速到最大速率v使它获得的最大动能为Ek.若带电粒子在A点的初速度、所受重力、通过狭缝的时间及C口的口径大小均可忽略不计,且不考虑相对论效应,则用该回旋加速器( )
回旋加速器在核科学、核技术、核医学等高新技术领域得到了广泛应用,有力地推动了现代科学技术的发展.回旋加速器的原理如图所示,D1和D2是两个正对的中空半圆金属盒,它们的半径均为R,且分别接在电压一定的交流电源两端,可在两金属盒之间的狭缝处形成变化的加速电场,两金属盒处于与盒面垂直、磁感应强度为B的匀强磁场中,A点处的粒子源不断产生带电粒子,它们在两盒之间被电场加速后在金属盒内的磁场中做匀速圆周运动.调节交流电源的频率,使得每当带电粒子运动到现金金属盒之间的狭缝边缘时恰好改变加速电场的方向.从而保证带电粒子能在两金属盒之间狭缝处总被加速,且最终都能沿位于D2盒边缘的C口射出.该回旋加速器可将原来静止的α粒子(氦原子核)加速到最大速率v使它获得的最大动能为Ek.若带电粒子在A点的初速度、所受重力、通过狭缝的时间及C口的口径大小均可忽略不计,且不考虑相对论效应,则用该回旋加速器( )| A. | 能使原来静止的质子获得的最大速率为$\frac{1}{2}$v | |
| B. | 能使原来静止的质子获得的动能为$\frac{1}{4}$Ek | |
| C. | 加速质子的交流电场频率与加速α粒子的交流电场频率之比为1:1 | |
| D. | 加速质子的总次数与加速α粒子总次数之比为2:1 |
 如图所示,粗心均匀的圆玻璃管两端封闭且竖直放置,玻璃管中的理想气体被一不导热的活塞分成两部分.当两部分气体温度均为T1=400K时,玻璃管下方气体的压强为上方气体压强的2倍,上方气体的体积是下方气体体积的2倍.为使上、下两部分气体的体积相等,保持上方气体温度不变,仅加热下方的气体,求下方气体的温度.
如图所示,粗心均匀的圆玻璃管两端封闭且竖直放置,玻璃管中的理想气体被一不导热的活塞分成两部分.当两部分气体温度均为T1=400K时,玻璃管下方气体的压强为上方气体压强的2倍,上方气体的体积是下方气体体积的2倍.为使上、下两部分气体的体积相等,保持上方气体温度不变,仅加热下方的气体,求下方气体的温度.