题目内容
2.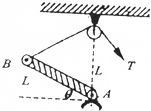 如图所示均匀杆AB长为L,可以绕转轴A点在竖直平面内自由转动,在A点正上方距离L处固定一个小定滑轮,细绳通过定滑轮与杆的另一端B相连,并将杆从水平位置缓慢向上拉起.已知杆水平时,细绳的拉力为T1,杆与水平面夹角为30°时,细绳的拉力为T2,则T1:T2是( )
如图所示均匀杆AB长为L,可以绕转轴A点在竖直平面内自由转动,在A点正上方距离L处固定一个小定滑轮,细绳通过定滑轮与杆的另一端B相连,并将杆从水平位置缓慢向上拉起.已知杆水平时,细绳的拉力为T1,杆与水平面夹角为30°时,细绳的拉力为T2,则T1:T2是( )| A. | $\sqrt{2}$:1 | B. | 2:1 | C. | 1:$\sqrt{2}$ | D. | 1:1 |
分析 找出杠杆即将离开水平位置和把吊桥拉起到与水平面的夹角为30°时的动力臂和阻力臂,然后结合利用杠杆的平衡条件分别求出T1、T2的大小.
解答  解:(1)杆在水平位置时,如图,△AOB和△ABE都为等腰直角三角形,则AE=BE
解:(1)杆在水平位置时,如图,△AOB和△ABE都为等腰直角三角形,则AE=BE
由于BE2+AE2=AB2
故AE=$\frac{{\sqrt{2}}}{2}L$,
由杠杆平衡可得:
T1×AE=G×AC,
T1=$\frac{G×AC}{AE}=\frac{{G×\frac{1}{2}L}}{{\frac{{\sqrt{2}}}{2}L}}=\frac{{\sqrt{2}}}{2}G$.
(2)把吊桥拉起到与水平面的夹角为30°时,如图: △ABO为等边三角形,AB=L,BE′=$\frac{1}{2}$L,
△ABO为等边三角形,AB=L,BE′=$\frac{1}{2}$L,
由于BE′2+AE′2=AB2
故AE′=$\frac{{\sqrt{3}}}{2}L$,
在△ACC′中,∠CAC′=30°,CC′=$\frac{1}{2}$AC=$\frac{1}{4}$L,
由于AC′2+CC′2=AC2,
故AC′=$\frac{\sqrt{3}}{4}$L,
根据杠杆平衡的条件可得:
T2×AE′=G×AC′,
T2=$G×\frac{AC′}{AE′}=G×\frac{{\frac{{\sqrt{3}}}{4}L}}{{\frac{{\sqrt{3}}}{2}L}}=\frac{1}{2}G$;
故T1:T2=$\frac{\sqrt{2}}{2}$G:$\frac{1}{2}$G=$\sqrt{2}$:1.
故选:A.
点评 本题考查考了杠杆平衡条件的应用,分析题意画出两种情况下的杠杆示意图是本题的关键,数学是基础!

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
13. 某学习小组的同学设计了如图甲所示的电路来测量定值电阻R0的阻值及某电源的电动势E和内阻r.实验器材有:
某学习小组的同学设计了如图甲所示的电路来测量定值电阻R0的阻值及某电源的电动势E和内阻r.实验器材有:
待测电源(电动势为E,内阻为r)
待测电阻R0,
电流表A(量程为0.6A,内阻不计),
电阻箱R(0~99.9Ω),
单刀单掷开关S1和S2,导线若干.
(1)先测电阻R0的阻值,请将学习小组同学的操作补充完整:先闭合S1和S2,调节电阻箱,读出其示数r1和对应的电流表示数I,然后断开S2,调节电阻箱阻值,使电流表的示数仍为I,读出此时电阻箱的示数r0,则电阻R0的表达式为R0=r1-r2.
(2)学习小组同学通过上述操作,测得电阻R0=9.5Ω,继续测电源的电动势E和内阻r,该小组同学的做法是:闭合S1,断开S2,多次调节电阻箱,读出多组电阻箱示数R和对应的电流表示数I,如下表数据:
①用图象法可以更准确的求出该电源的电动势和内阻,请根据以上数据完善坐标系(标出纵轴所代表的物理量和相对应的刻度),并描点连线,要求所描图线为直线,以便于研究其规律.
②利用上述图象可求出该电源的电动势E=6.0V,r=2.5Ω.
 某学习小组的同学设计了如图甲所示的电路来测量定值电阻R0的阻值及某电源的电动势E和内阻r.实验器材有:
某学习小组的同学设计了如图甲所示的电路来测量定值电阻R0的阻值及某电源的电动势E和内阻r.实验器材有:待测电源(电动势为E,内阻为r)
待测电阻R0,
电流表A(量程为0.6A,内阻不计),
电阻箱R(0~99.9Ω),
单刀单掷开关S1和S2,导线若干.
(1)先测电阻R0的阻值,请将学习小组同学的操作补充完整:先闭合S1和S2,调节电阻箱,读出其示数r1和对应的电流表示数I,然后断开S2,调节电阻箱阻值,使电流表的示数仍为I,读出此时电阻箱的示数r0,则电阻R0的表达式为R0=r1-r2.
(2)学习小组同学通过上述操作,测得电阻R0=9.5Ω,继续测电源的电动势E和内阻r,该小组同学的做法是:闭合S1,断开S2,多次调节电阻箱,读出多组电阻箱示数R和对应的电流表示数I,如下表数据:
| 组数 | 1 | 2 | 3 | 4 | 5 |
| 电阻R/Ω | 00 | 3.0 | 6.0 | 12.0 | 18.0 |
| 电流I/A | 0.50 | 0.40 | 0.33 | 0.25 | 0.20 |
②利用上述图象可求出该电源的电动势E=6.0V,r=2.5Ω.
10. 如图所示,在地球表面附近的A点发射卫星,当发射速度为v1时卫星的轨道刚好为近地圆轨道1,当发射速度为v3时卫星恰好脱离地球的引力变为了绕太阳运动的小行星,则以下说法正确的是:( )
如图所示,在地球表面附近的A点发射卫星,当发射速度为v1时卫星的轨道刚好为近地圆轨道1,当发射速度为v3时卫星恰好脱离地球的引力变为了绕太阳运动的小行星,则以下说法正确的是:( )
 如图所示,在地球表面附近的A点发射卫星,当发射速度为v1时卫星的轨道刚好为近地圆轨道1,当发射速度为v3时卫星恰好脱离地球的引力变为了绕太阳运动的小行星,则以下说法正确的是:( )
如图所示,在地球表面附近的A点发射卫星,当发射速度为v1时卫星的轨道刚好为近地圆轨道1,当发射速度为v3时卫星恰好脱离地球的引力变为了绕太阳运动的小行星,则以下说法正确的是:( )| A. | 轨道3对应的发射速度v3为7.9km/s | |
| B. | 轨道1对应的发射速度v1为7.9km/s | |
| C. | 轨道2对应的发射速度为可能为14.5km/s | |
| D. | 轨道2对应的发射速度为可能为10.8km/s |
17. 如图为圆盘发电机的示意图,钢盘绕水平的铜轴C在垂直于盘面的匀强磁场中匀速转动,铜片D与铜盘的边缘接触,铜盘、导线和电阻R连接组成电路,则( )
如图为圆盘发电机的示意图,钢盘绕水平的铜轴C在垂直于盘面的匀强磁场中匀速转动,铜片D与铜盘的边缘接触,铜盘、导线和电阻R连接组成电路,则( )
 如图为圆盘发电机的示意图,钢盘绕水平的铜轴C在垂直于盘面的匀强磁场中匀速转动,铜片D与铜盘的边缘接触,铜盘、导线和电阻R连接组成电路,则( )
如图为圆盘发电机的示意图,钢盘绕水平的铜轴C在垂直于盘面的匀强磁场中匀速转动,铜片D与铜盘的边缘接触,铜盘、导线和电阻R连接组成电路,则( )| A. | 转动过程电能转化为机械能 | B. | D处的电势比C处高 | ||
| C. | 通过R的电流方向从A指向B | D. | 产生的电动势大小与角速度ω有关 |
12.一辆汽车先以速度V1匀速行驶了甲、乙两地距离的2/3,接着以速度V2匀速走完了剩余的路程,则汽车在全程中的平均速度是( )
| A. | $\frac{{{3v}_{1}v}_{2}}{{2v}_{2}{+v}_{1}}$ | B. | $\frac{{2v}_{1}{+v}_{2}}{6}$ | C. | $\frac{{v}_{1}{+v}_{2}}{2}$ | D. | $\frac{{2v}_{1}{+v}_{2}}{2}$ |
 矩形线圈在匀强磁场中匀速旋转时,产生的感应电动势最大值为50V,那么该线圈由如图所示的位置转过30°时,线圈中的感应电动势大小为$25\sqrt{3}$V,由如图所示的位置转过90°时,线圈中的感应电动势大小为0.
矩形线圈在匀强磁场中匀速旋转时,产生的感应电动势最大值为50V,那么该线圈由如图所示的位置转过30°时,线圈中的感应电动势大小为$25\sqrt{3}$V,由如图所示的位置转过90°时,线圈中的感应电动势大小为0. 如图所示的电路中.电源两端电压U保持不变.当闭合开关S后,将滑动变阻器的滑片P置于a端时(a、b是滑动变阻器的两个端点),电压表的示数为U1,电流表的示数I1为1A,电阻R1消耗的电功率P1为6W,电阻R2消耗的电功率为P2.当闭合开关S后,将滑动变阻器的滑片P置于b端时,电压表的示数为U2,电流表的示数为I2,电阻R2消耗的电功率为P2′.已知P2:P2′=1:9,U1:U2=7:3.求:
如图所示的电路中.电源两端电压U保持不变.当闭合开关S后,将滑动变阻器的滑片P置于a端时(a、b是滑动变阻器的两个端点),电压表的示数为U1,电流表的示数I1为1A,电阻R1消耗的电功率P1为6W,电阻R2消耗的电功率为P2.当闭合开关S后,将滑动变阻器的滑片P置于b端时,电压表的示数为U2,电流表的示数为I2,电阻R2消耗的电功率为P2′.已知P2:P2′=1:9,U1:U2=7:3.求: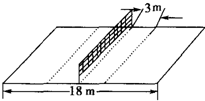 如图所示,女排比赛时,排球场总长为18m,设球网高度为2m,运动员站在网前3m处正对球网跳起将球水平击出.
如图所示,女排比赛时,排球场总长为18m,设球网高度为2m,运动员站在网前3m处正对球网跳起将球水平击出.