题目内容
14.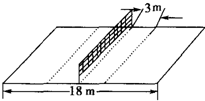 如图所示,女排比赛时,排球场总长为18m,设球网高度为2m,运动员站在网前3m处正对球网跳起将球水平击出.
如图所示,女排比赛时,排球场总长为18m,设球网高度为2m,运动员站在网前3m处正对球网跳起将球水平击出.(1)若击球的高度为2.5m,为使球既不触网又不越界,求球的初速度范围.
(2)当击球点的高度为何值时,无论水平击球的速度多大,球不是触网就是越界?
分析 (1)排球飞出后做平抛运动,抓住两个临界情况,即刚好不触网和不越界,由竖直高度可确定时间,根据水平位移可求得排球的速度范围;
(2)抓住临界状态,即此时既不触网也不越界,结合平抛运动的规律求出临界高度.
解答 解:(1)当球刚好不触网时,根据${h}_{1}-h=\frac{1}{2}g{{t}_{1}}^{2}$得:${t}_{1}=\sqrt{\frac{2({h}_{1}-h)}{g}}=\sqrt{\frac{2×(2.5-2)}{10}}s=\frac{\sqrt{10}}{10}s$,
则平抛运动的最小速度为:${v}_{min}=\frac{{x}_{1}}{{t}_{1}}=\frac{3}{\frac{\sqrt{10}}{10}}m/s=3\sqrt{10}m/s$.
当球刚好不越界时,根据${h}_{1}=\frac{1}{2}g{{t}_{2}}^{2}$得:${t}_{2}=\sqrt{\frac{2{h}_{1}}{g}}=\sqrt{\frac{2×2.5}{10}}s=\frac{\sqrt{2}}{2}s$,
则平抛运动的最大速度为:${v}_{max}=\frac{{x}_{2}}{{t}_{2}}=\frac{9+3}{\frac{\sqrt{2}}{2}}m/s=12\sqrt{2}m/s$,
水平击球的速度范围为$3\sqrt{10}m/s<v≤12\sqrt{2}m/s$.
(2)设击球点的高度为H.当H较小时,击球速度过大会出界,击球速度过小又会触网,情况是球刚好擦网而过,落地时又恰压底线上,则有:
$\frac{{x}_{1}}{\sqrt{\frac{2H}{g}}}=\frac{{x}_{2}}{\sqrt{\frac{2(H-h)}{g}}}$,
其中x1=12m,x2=3m,h=2m,
代入数据解得:h=2.13m,
即击球高度不超过此值时,球不是出界就是触网.
答:(1)球的初速度范围为$3\sqrt{10}m/s<v≤12\sqrt{2}m/s$.
(2)当击球点的高度为2.13m时,无论水平击球的速度多大,球不是触网就是越界.
点评 本题考查平抛运动在生活中应用,要通过分析找出临界条件,由平抛运动的规律即可求解.

| A. | 电源向外提供的电能越多,表示电动势越大 | |
| B. | 电动势就是电源两端的电压 | |
| C. | 电源的电动势与外电路有关.外电路电阻越大,电动势就越大 | |
| D. | 电动势越大的电源,将其他形式的能转化为电能的本领越大 |
| A. | 力是矢量,位移是矢量,所以功也是矢量 | |
| B. | 功有正、负之分,所以功也有方向性 | |
| C. | 若某一个力对物体不做功,说明该物体一定没有位移 | |
| D. | 一个力对物体做的功等于这个力的大小、物体位移大小及力和位移间夹角的余弦三者的乘积 |
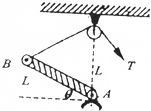 如图所示均匀杆AB长为L,可以绕转轴A点在竖直平面内自由转动,在A点正上方距离L处固定一个小定滑轮,细绳通过定滑轮与杆的另一端B相连,并将杆从水平位置缓慢向上拉起.已知杆水平时,细绳的拉力为T1,杆与水平面夹角为30°时,细绳的拉力为T2,则T1:T2是( )
如图所示均匀杆AB长为L,可以绕转轴A点在竖直平面内自由转动,在A点正上方距离L处固定一个小定滑轮,细绳通过定滑轮与杆的另一端B相连,并将杆从水平位置缓慢向上拉起.已知杆水平时,细绳的拉力为T1,杆与水平面夹角为30°时,细绳的拉力为T2,则T1:T2是( )| A. | $\sqrt{2}$:1 | B. | 2:1 | C. | 1:$\sqrt{2}$ | D. | 1:1 |
 如图所示,质量m=1kg的物块A放在质量M=4kg木板B的左端,起初A、B静止在水平地面上,现用一水平向左的力F作用在木板B上,已知AB之间的动摩擦因数为μ1=0.4,地面与B之间的动摩擦因数为μ2=0.1,假设最大静摩擦力等于滑动摩擦力,g=10m/s2.求:
如图所示,质量m=1kg的物块A放在质量M=4kg木板B的左端,起初A、B静止在水平地面上,现用一水平向左的力F作用在木板B上,已知AB之间的动摩擦因数为μ1=0.4,地面与B之间的动摩擦因数为μ2=0.1,假设最大静摩擦力等于滑动摩擦力,g=10m/s2.求: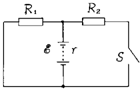 如图所示,当开关S闭合时,电源内外电路消耗的总功率为24W,外电路消耗的功率为20W,电源内电阻r=1Ω,电阻R1=11Ω,则R1消耗的功率为9W(保留整数);当开关S断开时,电源内外电路消耗的总功率为12W.
如图所示,当开关S闭合时,电源内外电路消耗的总功率为24W,外电路消耗的功率为20W,电源内电阻r=1Ω,电阻R1=11Ω,则R1消耗的功率为9W(保留整数);当开关S断开时,电源内外电路消耗的总功率为12W.