题目内容
8.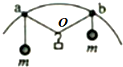 如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )
如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )| A. | 细绳aO段与竖直方向的夹角为60° | B. | 细绳aO段与竖直方向的夹角为30° | ||
| C. | 小物块的质量为m | D. | 小物块的质量为2m |
分析 同一根绳子上的张力大小相等,根据ab距离等于圆环半径,可求出绳aO与竖直方向所成角度,由平衡条件求小物块的质量.
解答  解:将圆弧补充完整,设圆心所在的位置为O′,由题意可知△abO′为等边三角形,根据几何知识可知∠aOb=120°,则细绳aO段与竖直方向的夹角为60°,故A正确,B错误;
解:将圆弧补充完整,设圆心所在的位置为O′,由题意可知△abO′为等边三角形,根据几何知识可知∠aOb=120°,则细绳aO段与竖直方向的夹角为60°,故A正确,B错误;
CD、在一根绳子上的拉力大小相等 T=mg,小物块受到两条绳子的拉力作用大小相等,夹角为120°,故受到的拉力合力等于mg,则小物块拉力的合力大小等于小物块的重力,即知小物块的质量为m.故C正确,D错误.
故选:AC
点评 解决本题关键是能根据题目给出的几何关系确认拉小物块的两绳夹角为120°,再根据两个大小相等互成120°两力的合成结论求解即可.

练习册系列答案
相关题目
18. 一辆汽车在平直的路面上启动,启动过程的v-t图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行于横轴的直线.已知从t1时刻开始汽车的功率达到额定功率且保持不变,整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )
一辆汽车在平直的路面上启动,启动过程的v-t图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行于横轴的直线.已知从t1时刻开始汽车的功率达到额定功率且保持不变,整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )
 一辆汽车在平直的路面上启动,启动过程的v-t图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行于横轴的直线.已知从t1时刻开始汽车的功率达到额定功率且保持不变,整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )
一辆汽车在平直的路面上启动,启动过程的v-t图象如图所示,其中OA段为直线,AB段为曲线,B点后为平行于横轴的直线.已知从t1时刻开始汽车的功率达到额定功率且保持不变,整个运动过程中汽车所受阻力的大小恒为Ff,以下说法正确的是( )| A. | 0-t1时间内,汽车做变加速运动 | B. | 0-t2时间内,汽车做匀加速运动 | ||
| C. | 汽车的额定功率P=Ffv1 | D. | 汽车的额定功率P=Ffv2 |
19. 如图所示,小球从水平位置静止释放,设小球通过最低点时的速度为v,角速度为ω,加速度为a,绳的拉力为T,那么随着绳子L的增长( )
如图所示,小球从水平位置静止释放,设小球通过最低点时的速度为v,角速度为ω,加速度为a,绳的拉力为T,那么随着绳子L的增长( )
 如图所示,小球从水平位置静止释放,设小球通过最低点时的速度为v,角速度为ω,加速度为a,绳的拉力为T,那么随着绳子L的增长( )
如图所示,小球从水平位置静止释放,设小球通过最低点时的速度为v,角速度为ω,加速度为a,绳的拉力为T,那么随着绳子L的增长( )| A. | v、a都增大 | B. | ω、a都减小 | C. | T、a都不变 | D. | v增大,ω减小 |
16.如图所示,可看成质点的a、b、c是在地球大气层外圆轨道上运动的3颗卫星,下列说法正确的是( )


| A. | b、c的线速度大小相等,且大于a的线速度 | |
| B. | b、c的向心加速度大小相等,且大于a的向心加速度 | |
| C. | b的发射速度一定大于a的发射速度 | |
| D. | b、c的角速度大小相等,且大于a的角速度 |
3.据报道,天文学家新发现了太阳系外的一颗行星.这颗行星的体积是地球的a倍,质量是地球的b倍.已知近地卫星绕地球运动的周期约为T,引力常量为G.则该行星的平均密度为( )
| A. | $\frac{3π}{G{T}^{2}}$ | B. | $\frac{π}{3{T}^{2}}$ | C. | $\frac{3πb}{aG{T}^{2}}$ | D. | $\frac{3πa}{bG{T}^{2}}$ |
13.美国科学家Willard S.Boyle与George E.Smith因电荷耦合器件(CCD)的重要发明荣获2009年度诺贝尔物理学奖.CCD是将光学量转变成电学量的传感器.下列器件不可作为传感器的是( )
| A. | 干簧管 | B. | 干电池 | C. | 霍尔元件 | D. | 热敏电阻 |
17.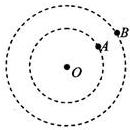 有A、B两颗卫星绕地心O做圆周运动,旋转方向相同.A卫星的周期为T1,如图所示在某一时刻两卫星相距最近,经时间t 他们再次相距最近,则B卫星的周期T2为( )
有A、B两颗卫星绕地心O做圆周运动,旋转方向相同.A卫星的周期为T1,如图所示在某一时刻两卫星相距最近,经时间t 他们再次相距最近,则B卫星的周期T2为( )
 有A、B两颗卫星绕地心O做圆周运动,旋转方向相同.A卫星的周期为T1,如图所示在某一时刻两卫星相距最近,经时间t 他们再次相距最近,则B卫星的周期T2为( )
有A、B两颗卫星绕地心O做圆周运动,旋转方向相同.A卫星的周期为T1,如图所示在某一时刻两卫星相距最近,经时间t 他们再次相距最近,则B卫星的周期T2为( )| A. | ${T_2}=\frac{{t{T_1}}}{{t+{T_1}}}$ | B. | ${T_2}=\frac{{t{T_1}}}{{t-{T_1}}}$ | C. | ${T_2}=\frac{T_1}{{t(t+{T_1})}}$ | D. | ${T_2}=\frac{T_1}{{t(t-{T_1})}}$ |
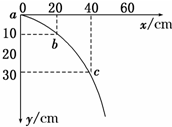 某同学在做平抛运动实验时得出如图所示的小球运动轨迹,a、b、c三点的位置在运动轨迹上已标出,g取10m/s2.则:
某同学在做平抛运动实验时得出如图所示的小球运动轨迹,a、b、c三点的位置在运动轨迹上已标出,g取10m/s2.则: