题目内容
3.据报道,天文学家新发现了太阳系外的一颗行星.这颗行星的体积是地球的a倍,质量是地球的b倍.已知近地卫星绕地球运动的周期约为T,引力常量为G.则该行星的平均密度为( )| A. | $\frac{3π}{G{T}^{2}}$ | B. | $\frac{π}{3{T}^{2}}$ | C. | $\frac{3πb}{aG{T}^{2}}$ | D. | $\frac{3πa}{bG{T}^{2}}$ |
分析 根据近地卫星绕地球运动的周期为T,运用万有引力提供向心力,求出地球的质量,再求出地球的密度.再根据行星与地球密度的关系求出行星的平均密度.
解答 解:对于近地卫星,设其质量为m,地球的质量为M,半径为R,则
根据万有引力提供向心力$G\frac{Mm}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}^{2}}$,解得地球的质量M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,地球的密度$ρ=\frac{M}{\frac{4π{R}^{3}}{3}}=\frac{3π}{G{T}^{2}}$,
密度公式为$ρ=\frac{M}{V}$,这颗行星的体积是地球的a倍,质量是地球的b倍,则密度是地球的$\frac{b}{a}$倍,可知行星的平均密度ρ=$\frac{3πb}{aG{T}^{2}}$.
故选:C.
点评 解决本题的关键会根据万有引力提供向心力,只要知道近地卫星的周期,即可求出地球的密度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 如图所示,在粗糙的水平面上有一个小物块,两个互相垂直的水平力F1,F2将物块缓慢从O点拉至A点,在此过程中F1,F2分别做了3J和4J的功,则这两个力的合力做功为( )
如图所示,在粗糙的水平面上有一个小物块,两个互相垂直的水平力F1,F2将物块缓慢从O点拉至A点,在此过程中F1,F2分别做了3J和4J的功,则这两个力的合力做功为( )
 如图所示,在粗糙的水平面上有一个小物块,两个互相垂直的水平力F1,F2将物块缓慢从O点拉至A点,在此过程中F1,F2分别做了3J和4J的功,则这两个力的合力做功为( )
如图所示,在粗糙的水平面上有一个小物块,两个互相垂直的水平力F1,F2将物块缓慢从O点拉至A点,在此过程中F1,F2分别做了3J和4J的功,则这两个力的合力做功为( )| A. | 7J | B. | 5J | C. | 4J | D. | 1J |
14.下列说法正确的是( )
| A. | 可以将工厂里扩散到外界的能量收集起来重新利用 | |
| B. | 分子间的距离增大时,分子间的引力和斥力都减小 | |
| C. | 气体对容器壁有压强是气体分子对容器壁频繁碰撞的结果 | |
| D. | 温度升高,说明物体中所有分子的动能都增大 | |
| E. | 在一个绝热容器内,不停地搅拌液体,可使液体的温度升高 |
11.下列说法正确的是( )
| A. | 第二类永动机不可能制成是因为它违反了能量守恒定律 | |
| B. | 在绝热条件下压缩理想气体,气体的内能一定增加 | |
| C. | 只要知道气体的摩尔体积和阿伏加德罗常数,就可以估算出气体分子的直径 | |
| D. | 一定质量的理想气体,压强不变、温度升高时,气体分子单位时间对气缸壁单位面积碰撞的次数将变少 |
18. 如图所示,长为R的轻杆一端拴有一个小球,另一端连在光滑的固定轴O上,现在最低点给小球一水平初速度,使小球能在竖直平面内做完整圆周运动,不计空气阻力,则( )
如图所示,长为R的轻杆一端拴有一个小球,另一端连在光滑的固定轴O上,现在最低点给小球一水平初速度,使小球能在竖直平面内做完整圆周运动,不计空气阻力,则( )
 如图所示,长为R的轻杆一端拴有一个小球,另一端连在光滑的固定轴O上,现在最低点给小球一水平初速度,使小球能在竖直平面内做完整圆周运动,不计空气阻力,则( )
如图所示,长为R的轻杆一端拴有一个小球,另一端连在光滑的固定轴O上,现在最低点给小球一水平初速度,使小球能在竖直平面内做完整圆周运动,不计空气阻力,则( )| A. | 小球通过最高点时的最小速度为$\sqrt{gR}$ | |
| B. | 若小球通过最高点时速度越大,则杆对小球的作用力越大 | |
| C. | 若小球在最高点的速度大小为$\sqrt{4gR}$,则此时杆对小球作用力向下 | |
| D. | 若小球在最低点的速度大小为$\sqrt{5gR}$,则小球通过最高点时对杆无作用力 |
8.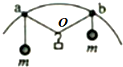 如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )
如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )
 如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )
如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )| A. | 细绳aO段与竖直方向的夹角为60° | B. | 细绳aO段与竖直方向的夹角为30° | ||
| C. | 小物块的质量为m | D. | 小物块的质量为2m |
15.下列说法正确的是( )
| A. | 机械波既有横波又有纵波,而电磁波只有纵波 | |
| B. | 在电磁波发射技术中,使电磁波随各种信号而改变叫解调 | |
| C. | 所有波都能发生干涉、衍射和多普勒效应 | |
| D. | 麦克斯韦首先提出了电磁波理论,并用实验证实了电磁波的存在 |
12.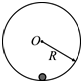 如图所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使它在瞬间得到一个水平初速度v0,v0大小不同则小球能够上升到的最大高度(距离底部)H也不同.下列说法中正确的是( )
如图所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使它在瞬间得到一个水平初速度v0,v0大小不同则小球能够上升到的最大高度(距离底部)H也不同.下列说法中正确的是( )
 如图所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使它在瞬间得到一个水平初速度v0,v0大小不同则小球能够上升到的最大高度(距离底部)H也不同.下列说法中正确的是( )
如图所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使它在瞬间得到一个水平初速度v0,v0大小不同则小球能够上升到的最大高度(距离底部)H也不同.下列说法中正确的是( )| A. | v0=$\sqrt{gR}$时,H=$\frac{R}{2}$ | B. | v0=$\sqrt{3gR}$时,H=$\frac{3R}{2}$ | C. | v0=$\sqrt{4gR}$时,H=2R | D. | v0=$\sqrt{5gR}$时,H=2R |
1.关于光的现象,下列说法正确的是( )
| A. | 光的偏振现象说明了光是一种横波 | |
| B. | 做单缝衍射实验时,单缝宽度变窄,衍射条纹间距变宽 | |
| C. | 医学上用激光来切除肿瘤是应用激光的平行度好的特点 | |
| D. | 增透膜主要应用了光的干涉原理 |