题目内容
17.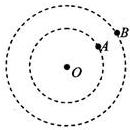 有A、B两颗卫星绕地心O做圆周运动,旋转方向相同.A卫星的周期为T1,如图所示在某一时刻两卫星相距最近,经时间t 他们再次相距最近,则B卫星的周期T2为( )
有A、B两颗卫星绕地心O做圆周运动,旋转方向相同.A卫星的周期为T1,如图所示在某一时刻两卫星相距最近,经时间t 他们再次相距最近,则B卫星的周期T2为( )| A. | ${T_2}=\frac{{t{T_1}}}{{t+{T_1}}}$ | B. | ${T_2}=\frac{{t{T_1}}}{{t-{T_1}}}$ | C. | ${T_2}=\frac{T_1}{{t(t+{T_1})}}$ | D. | ${T_2}=\frac{T_1}{{t(t-{T_1})}}$ |
分析 两行星相距最近时,两行星应该在同一半径方向上,两行星相距最远时,两行星应该在同一直径上,由于A的周期小,故A转得较快,当A比B多转一圈时两行星再次相距最近.
解答 解:两行星相距最近时,两行星应该在同一半径方向上,A多转动一圈时,第二次追上,转动的角度相差2π,即:
$\frac{2π}{{T}_{1}}$•t-$\frac{2π}{{T}_{2}}$•t=2π,
解得:${T_2}=\frac{{t{T_1}}}{{t-{T_1}}}$.故ACD错误,B正确;
故选:B
点评 根据几何关系得到两颗卫星相距最近和相距最远所满足的角度关系,最近时两卫星在同一半径上角度差为2π弧度,卫星相距最远时,两卫星在同一直径上,转过的角度差为π弧度.

练习册系列答案
相关题目
8.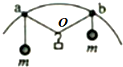 如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )
如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )
 如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )
如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )| A. | 细绳aO段与竖直方向的夹角为60° | B. | 细绳aO段与竖直方向的夹角为30° | ||
| C. | 小物块的质量为m | D. | 小物块的质量为2m |
5. 如图所示,两个同种玻璃制成的棱镜,顶角α1<α2,两单色光1和2分别垂直入射三棱镜,其出射光线与第二界面的夹角β1=β2,则下列判断正确的是( )
如图所示,两个同种玻璃制成的棱镜,顶角α1<α2,两单色光1和2分别垂直入射三棱镜,其出射光线与第二界面的夹角β1=β2,则下列判断正确的是( )
 如图所示,两个同种玻璃制成的棱镜,顶角α1<α2,两单色光1和2分别垂直入射三棱镜,其出射光线与第二界面的夹角β1=β2,则下列判断正确的是( )
如图所示,两个同种玻璃制成的棱镜,顶角α1<α2,两单色光1和2分别垂直入射三棱镜,其出射光线与第二界面的夹角β1=β2,则下列判断正确的是( )| A. | 在棱镜中1光的折射率比2光小 | |
| B. | 在棱镜中光1的传播速度比光2的小 | |
| C. | 以相同角度斜射到同一平行玻璃板,光2侧移量大 | |
| D. | 以相同的入射角从水中射入空气,在空气中只能看到一种光时,一定是光2 |
12.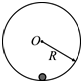 如图所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使它在瞬间得到一个水平初速度v0,v0大小不同则小球能够上升到的最大高度(距离底部)H也不同.下列说法中正确的是( )
如图所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使它在瞬间得到一个水平初速度v0,v0大小不同则小球能够上升到的最大高度(距离底部)H也不同.下列说法中正确的是( )
 如图所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使它在瞬间得到一个水平初速度v0,v0大小不同则小球能够上升到的最大高度(距离底部)H也不同.下列说法中正确的是( )
如图所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使它在瞬间得到一个水平初速度v0,v0大小不同则小球能够上升到的最大高度(距离底部)H也不同.下列说法中正确的是( )| A. | v0=$\sqrt{gR}$时,H=$\frac{R}{2}$ | B. | v0=$\sqrt{3gR}$时,H=$\frac{3R}{2}$ | C. | v0=$\sqrt{4gR}$时,H=2R | D. | v0=$\sqrt{5gR}$时,H=2R |
14.电场强度的定义式为E=$\frac{F}{q}$,点电荷的场强公式为E=$\frac{kQ}{{r}^{2}}$,下列说法中正确的是( )
| A. | E=$\frac{F}{q}$中的场强E是电荷q产生的 | B. | E=$\frac{F}{q}$中的场强E的方向和F方向相同 | ||
| C. | 由E=$\frac{F}{q}$可知E与F成正比,与q成反比 | D. | E=$\frac{kQ}{{r}^{2}}$中的场强E是电荷Q产生的 |
 光滑的水平面上,一物体在F=8N的水平拉力作用下由静止开始做匀加速直线运动,2s内发生的位移为x=8m,求:
光滑的水平面上,一物体在F=8N的水平拉力作用下由静止开始做匀加速直线运动,2s内发生的位移为x=8m,求: 如图所示,竖直面内的曲线轨道AB光滑,它的最低点B的切线沿水平方向,且与一位于同一竖直面内、半径R=1m的粗糙圆形轨道平滑连接.现有一质量m=3kg的滑块(可视为质点),从位于轨道上的A点由静止开始滑下,滑块经B点后恰好能通过圆形轨道的最高点C.已知A点到B点的高度h=3m,重力加速度g=10m/s2,空气阻力可忽略不计,求:
如图所示,竖直面内的曲线轨道AB光滑,它的最低点B的切线沿水平方向,且与一位于同一竖直面内、半径R=1m的粗糙圆形轨道平滑连接.现有一质量m=3kg的滑块(可视为质点),从位于轨道上的A点由静止开始滑下,滑块经B点后恰好能通过圆形轨道的最高点C.已知A点到B点的高度h=3m,重力加速度g=10m/s2,空气阻力可忽略不计,求: