题目内容
19.如图1所示,两根相距为L=2.0m的金属轨道固定于水平面上,导轨电阻不计,一根质量为m=1.0kg、长为L=2.0m、电阻为r=2.0Ω的金属棒两端放于导轨上,导轨与金属棒间的动摩擦因数为μ=0.20,棒与导轨的接触电阻不计.导轨左端连有阻值为R=4.0Ω的电阻,在电阻两端接有电压传感器并与计算机相连.有n段垂直导轨平面的宽度为c=3.0m,间距为d=2.0m的匀强磁场,磁感强度大小为B=1.0T,方向垂直纸面向里.金属棒初始位于OO'处,与第一段磁场相距s=6.0m.(g取10m/s2)
(1)若金属棒有向右的初速度v0=3.0m/s,为使金属棒保持匀速直线运动一直向右穿过各磁场,需对金属棒施加一个水平向右的拉力,求金属棒进入磁场前拉力F1的大小和进入磁场后拉力F2的大小;
(2)在(1)问的情况下,求金属棒从OO′开始运动到刚离开第10段磁场过程中,拉力所做的功;
(3)若金属棒初速度为零,现对棒施以水平向右的恒定拉力F=4.0N,使棒穿过各段磁场,发现计算机显示出的电压随时间以固定的周期做周期性变化,图象如图2所示(从金属棒进入第一段磁场开始计时,图中虚线与时间轴平行).求金属棒每穿过一个磁场过程中回路中产生的焦耳热,以及金属棒从第10段磁场穿出时的速度.
分析 (1)金属棒在进入磁场前,不受安培力作用,匀速运动时,拉力与摩擦力平衡;在进入磁场后,金属棒切割磁感线,产生感应电流,要保持匀速运动,拉力必须与摩擦力、安培力平衡.根据平衡条件和电磁感应知识,可求出拉力.
(2)利用功的公式,求出拉力做的总功.
(3)进入磁场前,拉力和摩擦力做功,根据动能定理,求出金属棒进入磁场时的速度.进入在磁场时,拉力、摩擦力和安培力做功,根据能量守恒定律求出焦耳热.由动能定理求解金属棒从第10段磁场穿出时的速度.
解答 解:(1)金属棒进入磁场前匀速运动,则有 F1=f=μN=μmg ①
代入解得 F1=2.0N ②
金属棒在磁场中运动时匀速运动,则有 F2=f+F安=f+BIL ③
又感应电流为 $I=\frac{E}{R+r}=\frac{{BL{v_0}}}{R+r}$ ④
联立得 ${F_2}=μmg+\frac{{{B^2}L{\;}^2{v_0}}}{R+r}$ ⑤
代入解得 F2=4.0N ⑥
(2)在非磁场区域外力F1所做的功为 W1=F1[s+(n-1)d]=μmg[s+(n-1)d]=48J ⑦
在磁场区域外力F2所做的功为 ${W_2}={F_2}×nc=({μmg+\frac{{{B^2}{L^2}{v_0}}}{R+r}})=120J$ ⑧
在此过程拉力所做的总功W=W1+W2=168J ⑨
(3)由电压的周期性分析知,进入每一段磁场的速度都相同,故在每一个周期中有△Ek=0,穿过每段磁场产生的电能E电均相同,所以(F-μmg)(c+d)=E电 ⑩
得Q=E电=10J (11)
进入每段磁场时的速度都相同,由动能定理得:$(F-μmg)s=\frac{1}{2}m{v_0}^2$ (12)
从每段磁场穿出的速度为v,根据动能定理得:$(F-μmg)c-W=\frac{1}{2}m{v^2}-\frac{1}{2}m{v_0}^2$ (13)
W=E电(14)
解得 v=4.0m/s(15)
答:
(1)金属棒进入磁场前拉力F1的大小是2.0N,进入磁场后拉力F2的大小是4.0N;
(2)金属棒从OO′开始运动到刚离开第10段磁场过程中,拉力所做的功为168J;
(3)金属棒每穿过一个磁场过程中回路中产生的焦耳热是10J,金属棒从第10段磁场穿出时的速度为4.0m/s.
点评 本题分析受力是基础,关键从能量转化和守恒角度来求解,解题时要注意抓住使棒进入各磁场的速度都相同,以及通过每段磁场时电路中发热量均相同的条件.

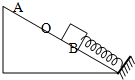 如图所示,一轻弹簧一端与挡板固定,另一端自由伸长时位于O点,当另一端和物块相连时,A、B是物块能保持静止的位置中离挡板最近和最远的点,A、B两点离挡板的距离分别是x1,x2,物块与斜面的最大静摩擦力为f,则弹簧的劲度系数为( )
如图所示,一轻弹簧一端与挡板固定,另一端自由伸长时位于O点,当另一端和物块相连时,A、B是物块能保持静止的位置中离挡板最近和最远的点,A、B两点离挡板的距离分别是x1,x2,物块与斜面的最大静摩擦力为f,则弹簧的劲度系数为( )| A. | $\frac{f}{{x}_{2}+{x}_{1}}$ | B. | $\frac{2f}{{x}_{2}+{x}_{1}}$ | C. | $\frac{2f}{{x}_{2}-{x}_{1}}$ | D. | $\frac{f}{{x}_{2}-{x}_{1}}$ |
 如图所示,用三块完全相同的两面平行的玻璃板组成一等边三角形(中间是空气),有红光和蓝光组成一细光束以平行底边BC从AB面射入,由AC面射出,则从AC面射出的光束( )
如图所示,用三块完全相同的两面平行的玻璃板组成一等边三角形(中间是空气),有红光和蓝光组成一细光束以平行底边BC从AB面射入,由AC面射出,则从AC面射出的光束( )| A. | 分成两束,上面为红光,下面为蓝光 | B. | 分成两束,上面为蓝光,下面为红光 | ||
| C. | 仍然为一束,并与底边BC平行 | D. | 仍然为一束,但向底边BC偏折 |
| A. | $\frac{E}{{c}^{2}}$ | B. | $\frac{2E}{111{c}^{2}}$ | C. | $\frac{113E}{111{c}^{2}}$ | D. | $\frac{2E}{{c}^{2}}$ |
| A. | α粒子散射实验表明原子具有核式结构 | |
| B. | 太阳辐射的能量主要来自太阳内部的核裂变 | |
| C. | 天然放射现象是由于原子核内部变化导致的 | |
| D. | 电子的发现表明原子不是构成物质的最小微粒 |
| A. | 整个过程中小球动量增量的大小为mgt | |
| B. | 整个过程中小球电势能变化了2mg2t2 | |
| C. | 从A点到最低点小球重力势能变化了$\frac{2m{g}^{2}{t}^{2}}{3}$ | |
| D. | 从加电场开始到小球运动到最低点时小球动能变化mg2t2 |
 如图所示,MN,PQ为水平放置的光滑金属导轨,导轨两端PM,QN连线均垂直于MN,PM=$\frac{1}{2}$L,QN=L.MN=2L,两根粗细相同长度均为L的金属棒AB、CD,垂直于导轨MN水平放置,两金属棒电阻均为R,整个装置处在竖直向下的匀强磁场中,磁感应强度为B,现金属棒AB、CD分别以速率v做相同的匀速运动,两金属棒在导轨上滑动时始终与导轨MN垂直,导轨电阻不计
如图所示,MN,PQ为水平放置的光滑金属导轨,导轨两端PM,QN连线均垂直于MN,PM=$\frac{1}{2}$L,QN=L.MN=2L,两根粗细相同长度均为L的金属棒AB、CD,垂直于导轨MN水平放置,两金属棒电阻均为R,整个装置处在竖直向下的匀强磁场中,磁感应强度为B,现金属棒AB、CD分别以速率v做相同的匀速运动,两金属棒在导轨上滑动时始终与导轨MN垂直,导轨电阻不计
 如图所示,物块A的质量为mA=2.0kg,沿光滑水平面以v0=6$\sqrt{3}$m/s速度水平向右匀速运动,离开平面后刚好落在静止在斜面上的木板B的最上端,且测得物块A所经轨迹到斜面的垂直距离最远.已知斜面足够长,倾角θ=30°,木板B的质量mB=2.0kg,A、B间的动摩擦因数μ1=$\frac{\sqrt{3}}{2}$,B与斜面间的动摩擦因数μ2=$\frac{2\sqrt{3}}{5}$,A在B上运动的过程中恰好没有滑离B木板,所有接触面间的最大摩擦力均等于滑运动摩擦力(g=10m/s2).求:
如图所示,物块A的质量为mA=2.0kg,沿光滑水平面以v0=6$\sqrt{3}$m/s速度水平向右匀速运动,离开平面后刚好落在静止在斜面上的木板B的最上端,且测得物块A所经轨迹到斜面的垂直距离最远.已知斜面足够长,倾角θ=30°,木板B的质量mB=2.0kg,A、B间的动摩擦因数μ1=$\frac{\sqrt{3}}{2}$,B与斜面间的动摩擦因数μ2=$\frac{2\sqrt{3}}{5}$,A在B上运动的过程中恰好没有滑离B木板,所有接触面间的最大摩擦力均等于滑运动摩擦力(g=10m/s2).求: