题目内容
11.静止的镭核${\;}_{86}^{226}$Ra发生α(${\;}_{2}^{4}$He)衰变,释放出的α粒子的动能为E,假设衰变时的能量全部以动能形式释放出来,则衰变过程中总的质量亏损是( )| A. | $\frac{E}{{c}^{2}}$ | B. | $\frac{2E}{111{c}^{2}}$ | C. | $\frac{113E}{111{c}^{2}}$ | D. | $\frac{2E}{{c}^{2}}$ |
分析 由动量守恒求出新核的动能,从而得到衰变释放的总能量,再由质能方程求出质量亏损.
解答 解:其衰变方程为:${\;}_{86}^{226}$Ra→${\;}_{84}^{222}$Rn+${\;}_{2}^{4}$He,
衰变满足动量守恒:mαVα=mRnVRn 即$\sqrt{2mαEkα}$=$\sqrt{2{m}_{α}{E}_{kα}}=\sqrt{2{m}_{{R}_{n}}{E}_{k{R}_{n}}}$,
所以EkRn=$\frac{4}{222}$E,所以总的动能为$\frac{222+4}{222}$E=$\frac{113}{111}$E,
这些能量就是由衰变过程的质量亏损而产生的,
所以亏损的质量为$\frac{113E}{111{c}^{2}}$.
故选:C.
点评 本题考查原子核发生α衰变时释放能量和质量亏损有关的知识,较难.本题还考查了动量和能量有关的知识.

练习册系列答案
相关题目
1. 如图所示,A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R0为定值电阻.当R2的滑片P在中间时,闭合开关S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势为E,内阻为r且恒定不变,那么,下列说法中正确的是( )
如图所示,A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R0为定值电阻.当R2的滑片P在中间时,闭合开关S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势为E,内阻为r且恒定不变,那么,下列说法中正确的是( )
 如图所示,A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R0为定值电阻.当R2的滑片P在中间时,闭合开关S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势为E,内阻为r且恒定不变,那么,下列说法中正确的是( )
如图所示,A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R0为定值电阻.当R2的滑片P在中间时,闭合开关S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势为E,内阻为r且恒定不变,那么,下列说法中正确的是( )| A. | 若将R2的滑动触头P向a端移动,θ将变大 | |
| B. | 若将R2的滑动触头P向b端移动,且用较强的光照射R1时,那么,小球重新达到稳定后θ将变小 | |
| C. | 若滑动触头P向b端移动,且用较弱的光照射R1时,那么,电压表的示数U的变化量的绝对值与电流表的示数I变化量的绝对值的比值将变大 | |
| D. | 若保持滑动触头P不动,且用较强的光照射R1时,那么,电压表的示数U的变化量的绝对值与电流表的示数I变化量的绝对值的比值不变 |
6.据报道,美国发射的“月球勘测轨道器”(LRO)每天在50km的高度穿越月球两极上空10次.若以T表示LRO在离月球表面高度h处的轨道上做匀速圆周运动的周期,以R表示月球的半径,则( )
| A. | LRO运行时的向心加速度为$\frac{{4{π^2}R}}{T^2}$ | |
| B. | LRO运行时的向心加速度$\frac{{4{π^2}(R+h)}}{T^2}$ | |
| C. | 月球表面的重力加速度为$\frac{{4{π^2}R}}{T^2}$ | |
| D. | 月球表面的重力加速度为$\frac{{4{π^2}{{(R+h)}^3}}}{{{T^2}{R^2}}}$ |
1. 如图所示,有一对等量异种电荷分别位于空间中的a点和f点,以a点和f点为顶点作一正立方体,现在各顶点间移动一试探电荷,关于试探电荷受电场力和具有的电势能以下判断正确的是( )
如图所示,有一对等量异种电荷分别位于空间中的a点和f点,以a点和f点为顶点作一正立方体,现在各顶点间移动一试探电荷,关于试探电荷受电场力和具有的电势能以下判断正确的是( )
 如图所示,有一对等量异种电荷分别位于空间中的a点和f点,以a点和f点为顶点作一正立方体,现在各顶点间移动一试探电荷,关于试探电荷受电场力和具有的电势能以下判断正确的是( )
如图所示,有一对等量异种电荷分别位于空间中的a点和f点,以a点和f点为顶点作一正立方体,现在各顶点间移动一试探电荷,关于试探电荷受电场力和具有的电势能以下判断正确的是( )| A. | 在b点和d点受力大小相等,方向相同 | |
| B. | 在c点和h点受力大小相等,方向相同 | |
| C. | 在b点和d点电势能相等 | |
| D. | 在c点和h点电势能相等 |
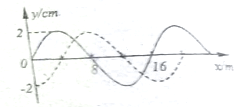 一列简谐横波沿x轴正方向传播,某时刻的波形如图中实线所示,经0.05s后,其波形如图中虚线所示,求:
一列简谐横波沿x轴正方向传播,某时刻的波形如图中实线所示,经0.05s后,其波形如图中虚线所示,求:
 如图所示,在地面附近,坐标系xOy在竖直平面内的空间中存在着沿水平方向垂直纸面向里的匀强磁场,磁感应强度为B,在x<0的空间内还有沿x轴负方向的匀强电场,场强大小为E.一个带正电的油滴经图中x轴上的M点,始终沿着与水平方向成θ=30°角的斜向下做直线运动,进入x>0区域.要使油滴进入x>0的区域后能在竖直平面内做匀速圆周运动,需要在x>0区域加一个匀强电场E′.若带电油滴做匀速圆周运动通过x轴上的N点,且MO=NO,g取l0m/s2.求:
如图所示,在地面附近,坐标系xOy在竖直平面内的空间中存在着沿水平方向垂直纸面向里的匀强磁场,磁感应强度为B,在x<0的空间内还有沿x轴负方向的匀强电场,场强大小为E.一个带正电的油滴经图中x轴上的M点,始终沿着与水平方向成θ=30°角的斜向下做直线运动,进入x>0区域.要使油滴进入x>0的区域后能在竖直平面内做匀速圆周运动,需要在x>0区域加一个匀强电场E′.若带电油滴做匀速圆周运动通过x轴上的N点,且MO=NO,g取l0m/s2.求: 在做测量电源电动势E和内阻r的实验时,提供的器材是:待测电源一个,内阻为RV的电压表一个(量程大于电源的电动势),电阻箱一个,开关一个,导线若干.
在做测量电源电动势E和内阻r的实验时,提供的器材是:待测电源一个,内阻为RV的电压表一个(量程大于电源的电动势),电阻箱一个,开关一个,导线若干. 如图所示,粗糙水平地面上有一压缩并锁定的弹簧,弹簧左端固定于竖直墙壁上,右端与一质量为m=0.1kg的小物块A(可视为质点)接触但不连接,光滑的固定圆周轨道MP与地面相切于M点,P点为轨道的最高点.现解除弹簧锁定,弹簧将小物块A推出,A沿粗糙水平地面运动,之后沿圆周轨道运动并恰能通过P点.已知A与地面间的动摩擦因数为μ=0.25,最初A与M点的距离L=2m,圆周轨道半径R=0.4m,g取10m/s2,空气阻力不计.求:
如图所示,粗糙水平地面上有一压缩并锁定的弹簧,弹簧左端固定于竖直墙壁上,右端与一质量为m=0.1kg的小物块A(可视为质点)接触但不连接,光滑的固定圆周轨道MP与地面相切于M点,P点为轨道的最高点.现解除弹簧锁定,弹簧将小物块A推出,A沿粗糙水平地面运动,之后沿圆周轨道运动并恰能通过P点.已知A与地面间的动摩擦因数为μ=0.25,最初A与M点的距离L=2m,圆周轨道半径R=0.4m,g取10m/s2,空气阻力不计.求: