题目内容
7.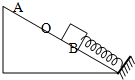 如图所示,一轻弹簧一端与挡板固定,另一端自由伸长时位于O点,当另一端和物块相连时,A、B是物块能保持静止的位置中离挡板最近和最远的点,A、B两点离挡板的距离分别是x1,x2,物块与斜面的最大静摩擦力为f,则弹簧的劲度系数为( )
如图所示,一轻弹簧一端与挡板固定,另一端自由伸长时位于O点,当另一端和物块相连时,A、B是物块能保持静止的位置中离挡板最近和最远的点,A、B两点离挡板的距离分别是x1,x2,物块与斜面的最大静摩擦力为f,则弹簧的劲度系数为( )| A. | $\frac{f}{{x}_{2}+{x}_{1}}$ | B. | $\frac{2f}{{x}_{2}+{x}_{1}}$ | C. | $\frac{2f}{{x}_{2}-{x}_{1}}$ | D. | $\frac{f}{{x}_{2}-{x}_{1}}$ |
分析 分别对物体处于对A、B点时进行受力分析,根据平衡条件列方程即可求解
解答 解:在沿斜面方向上,根据平衡条件有:k(x0-x1)=f+mgsinθ
同理,在B点,根据平衡有:k(x2-x0)+mgsinθ=f
联立解得:k=$\frac{2f}{{x}_{2}-{x}_{1}}$.
故选:C.
点评 本题考查了胡克定律和共点力平衡的综合运用,抓住两个临界状态,结合共点力平衡进行求解.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
17. 一电阻为R的金属线圈放入磁场中,穿过线圈的磁通量随时间的变化如图所示,在0-t0时间内通过线圈上某位置横截面的电荷量为q,则( )
一电阻为R的金属线圈放入磁场中,穿过线圈的磁通量随时间的变化如图所示,在0-t0时间内通过线圈上某位置横截面的电荷量为q,则( )
 一电阻为R的金属线圈放入磁场中,穿过线圈的磁通量随时间的变化如图所示,在0-t0时间内通过线圈上某位置横截面的电荷量为q,则( )
一电阻为R的金属线圈放入磁场中,穿过线圈的磁通量随时间的变化如图所示,在0-t0时间内通过线圈上某位置横截面的电荷量为q,则( )| A. | q=$\frac{{Φ}_{0}}{2R}$ | B. | q=$\frac{{Φ}_{0}}{R}$ | C. | q<$\frac{{Φ}_{0}}{R}$ | D. | q>$\frac{{Φ}_{0}}{R}$ |
18. 如图所示,在倾角为θ的足够长的固定光滑斜面上放置一质量为m的滑块,滑块上固定一“T”形杆,杆上用细线悬挂一个小球,当滑块和小球沿斜面运动达到稳定状态(小球与滑块相对静止)时,不计空气阻力,则悬线的方向应该是( )
如图所示,在倾角为θ的足够长的固定光滑斜面上放置一质量为m的滑块,滑块上固定一“T”形杆,杆上用细线悬挂一个小球,当滑块和小球沿斜面运动达到稳定状态(小球与滑块相对静止)时,不计空气阻力,则悬线的方向应该是( )
 如图所示,在倾角为θ的足够长的固定光滑斜面上放置一质量为m的滑块,滑块上固定一“T”形杆,杆上用细线悬挂一个小球,当滑块和小球沿斜面运动达到稳定状态(小球与滑块相对静止)时,不计空气阻力,则悬线的方向应该是( )
如图所示,在倾角为θ的足够长的固定光滑斜面上放置一质量为m的滑块,滑块上固定一“T”形杆,杆上用细线悬挂一个小球,当滑块和小球沿斜面运动达到稳定状态(小球与滑块相对静止)时,不计空气阻力,则悬线的方向应该是( )| A. | 沿竖直方向 | |
| B. | 与斜面垂直 | |
| C. | 与竖直方向成夹角α,且α<θ | |
| D. | 悬线的方向与小球的质量有关,不确定 |
17.P、Q为介质中的两个质点,一列简谐横波沿x轴正方向由P传到Q,图甲为该列简谐横波某一时刻的波形图,图乙为P、Q两质点的振动图象,则P、Q两质点平衡位置之间的距离可能是下列的哪些数值( )


| A. | 0.5m | B. | 1.5 m | C. | 2.5m | D. | 3.5m |

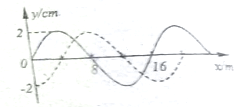 一列简谐横波沿x轴正方向传播,某时刻的波形如图中实线所示,经0.05s后,其波形如图中虚线所示,求:
一列简谐横波沿x轴正方向传播,某时刻的波形如图中实线所示,经0.05s后,其波形如图中虚线所示,求: 如图所示,甲、乙两人分别站在赤道和纬度为45°的地面上,已知地球的半径R=6400km,则甲、乙两人的线速度各是多少?
如图所示,甲、乙两人分别站在赤道和纬度为45°的地面上,已知地球的半径R=6400km,则甲、乙两人的线速度各是多少?
 如图所示,在地面附近,坐标系xOy在竖直平面内的空间中存在着沿水平方向垂直纸面向里的匀强磁场,磁感应强度为B,在x<0的空间内还有沿x轴负方向的匀强电场,场强大小为E.一个带正电的油滴经图中x轴上的M点,始终沿着与水平方向成θ=30°角的斜向下做直线运动,进入x>0区域.要使油滴进入x>0的区域后能在竖直平面内做匀速圆周运动,需要在x>0区域加一个匀强电场E′.若带电油滴做匀速圆周运动通过x轴上的N点,且MO=NO,g取l0m/s2.求:
如图所示,在地面附近,坐标系xOy在竖直平面内的空间中存在着沿水平方向垂直纸面向里的匀强磁场,磁感应强度为B,在x<0的空间内还有沿x轴负方向的匀强电场,场强大小为E.一个带正电的油滴经图中x轴上的M点,始终沿着与水平方向成θ=30°角的斜向下做直线运动,进入x>0区域.要使油滴进入x>0的区域后能在竖直平面内做匀速圆周运动,需要在x>0区域加一个匀强电场E′.若带电油滴做匀速圆周运动通过x轴上的N点,且MO=NO,g取l0m/s2.求: