题目内容
14. 如图所示,物块A的质量为mA=2.0kg,沿光滑水平面以v0=6$\sqrt{3}$m/s速度水平向右匀速运动,离开平面后刚好落在静止在斜面上的木板B的最上端,且测得物块A所经轨迹到斜面的垂直距离最远.已知斜面足够长,倾角θ=30°,木板B的质量mB=2.0kg,A、B间的动摩擦因数μ1=$\frac{\sqrt{3}}{2}$,B与斜面间的动摩擦因数μ2=$\frac{2\sqrt{3}}{5}$,A在B上运动的过程中恰好没有滑离B木板,所有接触面间的最大摩擦力均等于滑运动摩擦力(g=10m/s2).求:
如图所示,物块A的质量为mA=2.0kg,沿光滑水平面以v0=6$\sqrt{3}$m/s速度水平向右匀速运动,离开平面后刚好落在静止在斜面上的木板B的最上端,且测得物块A所经轨迹到斜面的垂直距离最远.已知斜面足够长,倾角θ=30°,木板B的质量mB=2.0kg,A、B间的动摩擦因数μ1=$\frac{\sqrt{3}}{2}$,B与斜面间的动摩擦因数μ2=$\frac{2\sqrt{3}}{5}$,A在B上运动的过程中恰好没有滑离B木板,所有接触面间的最大摩擦力均等于滑运动摩擦力(g=10m/s2).求:(1)A平抛运动的时间;
(2)木板B的长度;
(3)A、B整个运动过程中损失的机械能.
分析 (1)将落在木板B上的速度分解为水平方向和竖直方向,根据平行四边形定则求出竖直分速度,结合速度时间公式求出平抛运动的时间.
(2)根据牛顿第二定律分别求出A、B在斜面上运动时的加速度,根据运动学公式求出相对运动的位移,从而得出A、B间因摩擦产生的内能.
(3)根据A、B间摩擦产生的热量以及B与斜面间摩擦产生的热量,求出整个运动过程中损失的机械能.
解答 解:(1)物块落在B上时,竖直方向上的分速度vy=v0tanθ,
则平抛运动的时间t=$\frac{{v}_{y}}{g}=\frac{{v}_{0}tanθ}{g}=\frac{6\sqrt{3}×\frac{\sqrt{3}}{3}}{10}s=0.6s$.
(2)A在B上运动的初速度${v}_{1}=\frac{{v}_{0}}{cos30°}=\frac{6\sqrt{3}}{\frac{\sqrt{3}}{2}}m/s=12m/s$
A在B上滑动的加速度${a}_{1}=\frac{{m}_{A}gsinθ-{μ}_{1}mAgcosθ}{{m}_{A}}$=gsinθ-μ1gcosθ=10×$\frac{1}{2}$-$\frac{\sqrt{3}}{2}×10×\frac{\sqrt{3}}{2}$=-2.5m/s2.
B运动的加速度${a}_{2}=\frac{{m}_{B}gsin30°+{μ}_{1}{m}_{A}gcos30°-{μ}_{2}({m}_{A}+{m}_{B})gcos30°}{{m}_{B}}$=0.5m/s2.
当两者速度相等时,A恰好没离开B,根据速度时间公式得,v1+a1t=a2t
解得t=$\frac{{v}_{1}}{{a}_{2}-{a}_{1}}=\frac{12}{0.5+2.5}s=4s$.
则A、B之间的相对位移大小$△x={v}_{1}t+\frac{1}{2}{a}_{1}{t}^{2}-\frac{1}{2}{a}_{2}{t}^{2}$=$12×4-\frac{1}{2}×2.5×16-\frac{1}{2}×0.5×16m$=24m,
故木板长度为24m
(3)A、B间由于摩擦产生的热量Q1=μ1mAgcos30°△x=360J.
在此过程中B的位移${x}_{2}=\frac{1}{2}{a}_{2}{t}^{2}=4m$,
则B与接触面间的摩擦力产生的热量Q2=μ2(mA+mB)gcos30°x2=96J
则△E=Q=Q1+Q2=360+96J=456J.
答:(1)A平抛运动的时间为0.6s;
(2)木板长度为24m;
(3)A、B整个运动过程中损失的机械能为456J.
点评 解决本题的关键理清A、B在整个过程中的运动规律,结合牛顿第二定律和运动学公式进行求解,知道物体的受力是解决本题的关键.

| A. | LRO运行时的向心加速度为$\frac{{4{π^2}R}}{T^2}$ | |
| B. | LRO运行时的向心加速度$\frac{{4{π^2}(R+h)}}{T^2}$ | |
| C. | 月球表面的重力加速度为$\frac{{4{π^2}R}}{T^2}$ | |
| D. | 月球表面的重力加速度为$\frac{{4{π^2}{{(R+h)}^3}}}{{{T^2}{R^2}}}$ |

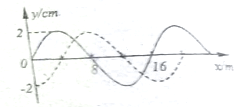 一列简谐横波沿x轴正方向传播,某时刻的波形如图中实线所示,经0.05s后,其波形如图中虚线所示,求:
一列简谐横波沿x轴正方向传播,某时刻的波形如图中实线所示,经0.05s后,其波形如图中虚线所示,求: 如图所示,斜面体倾角a=37°,在斜面顶端h=1.8m处有一质量为m=2.0kg、可视为质点的物体,斜面体质量为M=10.0kg,地面与斜面体间的动摩擦因数μ=0.15,斜面前方有一高l=1.0m的木桩DE.(重力加速度g取10m/s2).
如图所示,斜面体倾角a=37°,在斜面顶端h=1.8m处有一质量为m=2.0kg、可视为质点的物体,斜面体质量为M=10.0kg,地面与斜面体间的动摩擦因数μ=0.15,斜面前方有一高l=1.0m的木桩DE.(重力加速度g取10m/s2).
 在做测量电源电动势E和内阻r的实验时,提供的器材是:待测电源一个,内阻为RV的电压表一个(量程大于电源的电动势),电阻箱一个,开关一个,导线若干.
在做测量电源电动势E和内阻r的实验时,提供的器材是:待测电源一个,内阻为RV的电压表一个(量程大于电源的电动势),电阻箱一个,开关一个,导线若干.