题目内容
20．
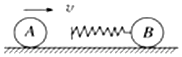如图所示，在光滑的水平面上放有两个小球A和B其质量mA＜mB，B球上固定一轻质弹簧．若将A球以速率v去碰撞静止的B球，碰撞时能量损失不计，下列说法中正确的是（ ）| A． | 当弹簧压缩量最大时，A球速率最小，B球速率最大 | |
| B． | 当弹簧恢复原长时，B球速率最大 | |
| C． | 当A球速率为零时，B球速率最大 | |
| D． | 当B球速率最大时，弹性势能不为零 |
分析 本题关键在于分析小球的运动过程：A与弹簧接触后，弹簧被压缩，弹簧对A产生向左的弹力，对B产生向右的弹力，A做减速运动，B做加速运动，当B的速度大于A的速度后，弹簧压缩量减小，则当小球A、B速度相等时，弹簧压缩量最大，弹性势能最大；当弹簧第一次恢复原长时，B球速率最大．
解答 解：分析小球的运动过程：A与弹簧接触后，弹簧被压缩，弹簧对A产生向左的弹力，对B产生向右的弹力，A做减速运动，B做加速运动，当B的速度等于A的速度时压缩量最大，此后A球速度继续减小，B球速度继续增大，弹簧压缩量减小，当弹簧第一次恢复原长时，B球速率最大．
A、由以上分析可知，当弹簧压缩量最大时，两球速度相同．故A错误；
B、弹簧倍压缩后，B球的速度一直在增大，当弹簧恢复原长时，B球速率达到最大值．故B正确；
C、由于质量mA＜mB，A的速度变化比B快，A球的速度是0时，弹簧仍然处于压缩状态，B球的速率没有达到最大．故C错误；
D、当弹簧恢复原长时，B球速率达到最大值，所以此时弹簧的弹性势能为0．故D错误．
故选：B
点评 本题是含有弹簧的问题，难点是对物体运动过程的分析，得到B球速度最大的临界条件，同时明确动量守恒定律的正确应用是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
5．2016年1月20日，美国天文学家推测，太阳系有第九大行星，该行星质量约为地球的10倍，半径约为地球的4倍，绕太阳一周需约2万年，冥王星比它亮约一万倍．已知地球的半径为R，地球表面的重力加速度为g，引力常量为G，地球和该行星绕太阳运动均视为匀速圆周运动．下列说法正确的是（ ）
| A． | 太阳的质量约为$\frac{g{R}^{2}}{G}$ | |
| B． | 该行星的质量约为$\frac{10g{R}^{2}}{G}$ | |
| C． | 该行星表面的重力加速度约为$\frac{5}{8}$g | |
| D． | 该行星到太阳的距离约为地球到太阳的距离的7.4×102倍 |
如图所示，在xoy平面的第一象限内加一垂直于纸面向外、磁感应强度为B的匀强磁场，一质量为m、带电荷量为q的正电粒子（重力不计）从坐标原点以速度v0射入第一象限，速度方向与x轴正向成37°角，粒子打在x轴上P点（图中未画出），若把磁场换为与xoy平面平行且与x轴正向成53°角斜向下的匀强方向，同一粒子仍从坐标原点以同一速度v0射入，粒子也打在P点，已知sin37°=0.6，cos37°=0.8，求：
8．
光滑水平面上有一静止的木块，子弹水平射入木块后未穿出，子弹和木块的v-t图象如图所示，已知木块质量大于子弹质量，从子弹射入木块到达到隐定状态，已知木块增加了50J动能，则此过程产生的内能可能是（ ）
光滑水平面上有一静止的木块，子弹水平射入木块后未穿出，子弹和木块的v-t图象如图所示，已知木块质量大于子弹质量，从子弹射入木块到达到隐定状态，已知木块增加了50J动能，则此过程产生的内能可能是（ ）| A． | 50J | B． | 70J | C． | 120J | D． | 180J |
15．奶粉的碳水化合物（糖）的含量是一个重要指标，可以用“旋光法”来测量糖溶液的浓度，从而鉴定含糖量．偏振光通过糖的水溶液后，偏振方向会相对于传播方向向左或向 右旋转一个角度 α，这一角度 α 称为“旋光度”，α 的值只与糖溶液的浓度有关，将 α 的测量值与标准值相比较，就能确定被测样品的含糖量了．如图所示，S 是自然光源，A、B 是偏振片，转动 B，使到达 O 处的光最强，然后将被测样品 P 置于 A、B 之间．以下说法中正 确的是（ ）
| A． | 到达 O 处光的强度会明显减弱 | |
| B． | 到达 O 处光的强度不会明显减弱 | |
| C． | 将偏振片 B 转动一个角度，使得 O 处光强度最大，偏振片 B 转过的角度等于 α | |
| D． | 将偏振片 A 转动一个角度，使得 O 处光强度最大，偏振片 A 转过的角度等于 α |
5．
如图所示，在发射地球同步卫星的过程中，卫星首先入椭圆轨道I，然后在Q点通过改变卫星速度，让卫星进入地球同步轨道II，则（ ）
如图所示，在发射地球同步卫星的过程中，卫星首先入椭圆轨道I，然后在Q点通过改变卫星速度，让卫星进入地球同步轨道II，则（ ）| A． | 该卫星的发射速度必定大于11.2km/s | |
| B． | 卫星在同步轨道II上的运行速度大于7.9km/s | |
| C． | 卫星在轨道I上经过Q点的速度小于在轨道II上经过Q点的速度 | |
| D． | 卫星在轨道I上的周期大于在轨道II的周期 |
12．质量为M的木块静止在足够宽大的光滑水平面上，一质量为m的子弹以速率v0水平向右射击木块，最后留在木块里，选向右的方向为正，对子弹射击木块这一过程，则有（ ）
| A． | 子弹和木块组成的系统动量守恒，机械能守恒 | |
| B． | 子弹和木块组成的系统动量守恒，机械能不守恒 | |
| C． | 子弹对木块的冲量与木块对子弹的冲量相同 | |
| D． | 木块对子弹的冲量为-$\frac{Mm{v}_{0}}{M+m}$ |
9．我国第一颗月球探测卫星“嫦娥一号”已于2007年10月24日在西昌卫星发射中心由“长征三号甲”运载火箭成功发射升空．假设该卫星的绕月轨道是圆形的，且距离月球表面高度为h，并已知该卫星的运行周期为T，月球直径为d，万有引力常量为G，则可求出（ ）
| A． | 月球质量M=$\frac{{{π}^{2}（d+2h）}^{3}}{{2GT}^{2}}$ | |
| B． | 月球探测卫星“嫦娥一号”在离月球表面h高度轨道上运行的速度v=$\frac{πd}{T}$ | |
| C． | 月球探测卫星“嫦娥一号”绕月轨道的半径r=d+h | |
| D． | 月球表面的重力加速度g=$\frac{2πd}{{T}^{2}}$ |
15．
质量为M和m0的滑块用轻弹簧连接，以恒定的速度v沿光滑水平面运动，与位于正对面的质量为m的静止滑块发生碰撞，如图所示，碰撞时间极短，在此过程中，下列说法可能发生的是（ ）
质量为M和m0的滑块用轻弹簧连接，以恒定的速度v沿光滑水平面运动，与位于正对面的质量为m的静止滑块发生碰撞，如图所示，碰撞时间极短，在此过程中，下列说法可能发生的是（ ）| A． | m0的速度不变，M和m的速度变为v1和v2，而且满足Mv=Mv1+mv2 | |
| B． | m0的速度不变，M、m的速度都变为v′，而且满足Mv=（M+m）v′ | |
| C． | M、m0、m速度均发生变化，分别为v1、v2、v3，而且满足（M+m0）v=Mv1+mv2+m0v3 | |
| D． | M、m、m0速度均发生变化，M和m0速度都变为v1，m的速度变为v2，而且满足（M+m0）v=（M+m0）v1+mv2 |