题目内容
8. 光滑水平面上有一静止的木块,子弹水平射入木块后未穿出,子弹和木块的v-t图象如图所示,已知木块质量大于子弹质量,从子弹射入木块到达到隐定状态,已知木块增加了50J动能,则此过程产生的内能可能是( )
光滑水平面上有一静止的木块,子弹水平射入木块后未穿出,子弹和木块的v-t图象如图所示,已知木块质量大于子弹质量,从子弹射入木块到达到隐定状态,已知木块增加了50J动能,则此过程产生的内能可能是( )| A. | 50J | B. | 70J | C. | 120J | D. | 180J |
分析 根据受力平衡得到动量守恒,进而得到前后速度的关系式,再由木块的动能变化得到内能的表达式,进而由图示速度大小关系得到内能的范围.
解答 解:设子弹质量为m,木块质量为M,子弹进入木块前的速度为v;
子弹射入木块的过程,子弹和木块整体的合外力为零,故动量守恒,所以,稳定状态的速度为:$v′=\frac{m}{m+M}v$;
又有从子弹射入木块到达到隐定状态,已知木块增加了50J动能,即为:$\frac{1}{2}Mv{′}^{2}=50J$;
所以,此过程产生的内能为:$Q=\frac{1}{2}m{v}^{2}-\frac{1}{2}(M+m)v{′}^{2}$=$\frac{1}{2}\frac{(M+m)^{2}}{m}v{′}^{2}-\frac{1}{2}(M+m)v{′}^{2}$=$\frac{1}{2}\frac{M}{m}(M+m)v{′}^{2}$=$\frac{M+m}{m}×50J$;
由图可知v>2v′,所以有:$\frac{M+m}{m}>2$,所以,Q>2×10J=100J,故AB错误,CD正确;
故选:CD.
点评 应用动量守恒定律前,要先验证系统的合外力为零,才能进行计算.

练习册系列答案
相关题目
13.一个人从深6米的水井中匀速取50N的水桶至地面后,在水平道路上行走了12m,再匀速走下8米的地下室,则此人用来提水桶的力所做的功为( )
| A. | 500J | B. | -500J | C. | -100J | D. | 100J |
3. 如图所示,两块相同的金属板正对着竖直放置,板长为L,板间距离为d.当两板间加电压U时,一个质量为m、电荷量为+q的带电粒子,以竖直速度v0从A点射人电场,经过一段时间后从B点射出电场,不计重力影响. 则( )
如图所示,两块相同的金属板正对着竖直放置,板长为L,板间距离为d.当两板间加电压U时,一个质量为m、电荷量为+q的带电粒子,以竖直速度v0从A点射人电场,经过一段时间后从B点射出电场,不计重力影响. 则( )
 如图所示,两块相同的金属板正对着竖直放置,板长为L,板间距离为d.当两板间加电压U时,一个质量为m、电荷量为+q的带电粒子,以竖直速度v0从A点射人电场,经过一段时间后从B点射出电场,不计重力影响. 则( )
如图所示,两块相同的金属板正对着竖直放置,板长为L,板间距离为d.当两板间加电压U时,一个质量为m、电荷量为+q的带电粒子,以竖直速度v0从A点射人电场,经过一段时间后从B点射出电场,不计重力影响. 则( )| A. | 带电粒子从A点运动到B点经历的时间为$\frac{L}{{v}_{0}}$ | |
| B. | 带电粒子经过B点时速度的大小$\frac{qUL}{md{v}_{0}}$ | |
| C. | A、B两点间的电势差$\frac{{q}^{2}{U}^{2}{L}^{2}}{2m{d}^{2}{{v}_{0}}^{2}}$ | |
| D. | 带电粒子从A点运动到B点,电势能减少$\frac{{q}^{2}{U}^{2}{L}^{2}}{2m{d}^{2}{{v}_{0}}^{2}}$ |
13.物理学家通过对实验的深入观察和研究,获得正确的科学认知,推动物理学的发展.下列说法符合事实的是( )
| A. | 玻尔通过一系列实验,证实了麦克斯韦关于光的电磁理论 | |
| B. | 查德威克用α粒子轰击${\;}_{7}^{14}$N获得反冲核${\;}_{8}^{17}$O,发现了中子 | |
| C. | 贝克勒尔发现的天然放射性现象,说明原子核有复杂结构 | |
| D. | 卢瑟福通过对阴极射线的研究,提出了原子核式结构模型 |
20.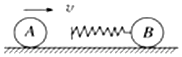 如图所示,在光滑的水平面上放有两个小球A和B其质量mA<mB,B球上固定一轻质弹簧.若将A球以速率v去碰撞静止的B球,碰撞时能量损失不计,下列说法中正确的是( )
如图所示,在光滑的水平面上放有两个小球A和B其质量mA<mB,B球上固定一轻质弹簧.若将A球以速率v去碰撞静止的B球,碰撞时能量损失不计,下列说法中正确的是( )
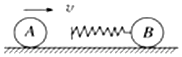 如图所示,在光滑的水平面上放有两个小球A和B其质量mA<mB,B球上固定一轻质弹簧.若将A球以速率v去碰撞静止的B球,碰撞时能量损失不计,下列说法中正确的是( )
如图所示,在光滑的水平面上放有两个小球A和B其质量mA<mB,B球上固定一轻质弹簧.若将A球以速率v去碰撞静止的B球,碰撞时能量损失不计,下列说法中正确的是( )| A. | 当弹簧压缩量最大时,A球速率最小,B球速率最大 | |
| B. | 当弹簧恢复原长时,B球速率最大 | |
| C. | 当A球速率为零时,B球速率最大 | |
| D. | 当B球速率最大时,弹性势能不为零 |
3. 质量为m1=1kg和m2(未知)的两个物体在光滑的水平面上正碰,碰撞时间极短,其x-t图象如图所示,则( )
质量为m1=1kg和m2(未知)的两个物体在光滑的水平面上正碰,碰撞时间极短,其x-t图象如图所示,则( )
 质量为m1=1kg和m2(未知)的两个物体在光滑的水平面上正碰,碰撞时间极短,其x-t图象如图所示,则( )
质量为m1=1kg和m2(未知)的两个物体在光滑的水平面上正碰,碰撞时间极短,其x-t图象如图所示,则( )| A. | 此碰撞一定为弹性碰撞 | B. | 被碰物体质量为3kg | ||
| C. | 碰后两物体速度相同 | D. | 此过程有机械能损失 |
 在原子核物理中,研究核子与核子关联的最有效途径是“双电荷交换反应”.这类反应的前半部分过程和下述力学模型类似.两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态.在它们左边有一垂直于轨道的固定挡板P,右边有一小球C沿轨道以速度v0射向B球,如图所示.C与B发生碰撞并立即结成一个整体D.在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变.然后,A球与挡板P发生碰撞,碰后A、D都静止不动,A与P接触而不粘连.过一段时间,突然解除锁定(锁定及解除锁定均无机械能损失).已知A球的质量为3m、B、C球的质量均为m.求:
在原子核物理中,研究核子与核子关联的最有效途径是“双电荷交换反应”.这类反应的前半部分过程和下述力学模型类似.两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态.在它们左边有一垂直于轨道的固定挡板P,右边有一小球C沿轨道以速度v0射向B球,如图所示.C与B发生碰撞并立即结成一个整体D.在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变.然后,A球与挡板P发生碰撞,碰后A、D都静止不动,A与P接触而不粘连.过一段时间,突然解除锁定(锁定及解除锁定均无机械能损失).已知A球的质量为3m、B、C球的质量均为m.求: 如图所示是骨伤科病房中一种常用的牵引装置,一根绳子跨过三个定滑轮A、B、C,悬挂一质量为M的重物,来牵引力病人的腿部,重力加速度为g,则在图示情况中,重物对绳子的拉力为Mg,病人脚部所受的拉力是$\sqrt{2}$Mg.(忽略滑轮的摩擦和重力)
如图所示是骨伤科病房中一种常用的牵引装置,一根绳子跨过三个定滑轮A、B、C,悬挂一质量为M的重物,来牵引力病人的腿部,重力加速度为g,则在图示情况中,重物对绳子的拉力为Mg,病人脚部所受的拉力是$\sqrt{2}$Mg.(忽略滑轮的摩擦和重力)