题目内容
11. 如图所示,在xoy平面的第一象限内加一垂直于纸面向外、磁感应强度为B的匀强磁场,一质量为m、带电荷量为q的正电粒子(重力不计)从坐标原点以速度v0射入第一象限,速度方向与x轴正向成37°角,粒子打在x轴上P点(图中未画出),若把磁场换为与xoy平面平行且与x轴正向成53°角斜向下的匀强方向,同一粒子仍从坐标原点以同一速度v0射入,粒子也打在P点,已知sin37°=0.6,cos37°=0.8,求:
如图所示,在xoy平面的第一象限内加一垂直于纸面向外、磁感应强度为B的匀强磁场,一质量为m、带电荷量为q的正电粒子(重力不计)从坐标原点以速度v0射入第一象限,速度方向与x轴正向成37°角,粒子打在x轴上P点(图中未画出),若把磁场换为与xoy平面平行且与x轴正向成53°角斜向下的匀强方向,同一粒子仍从坐标原点以同一速度v0射入,粒子也打在P点,已知sin37°=0.6,cos37°=0.8,求:(1)P点的坐标;
(2)匀强电场的电场强度.
分析 (1)根据洛伦兹力提供向心力求出半径公式,再跟几何关系联立即可求出P点坐标;
(2)粒子在该电场中做类平抛运动,利用运动的合成和分解几何牛顿第二定律及运动学规律联立即可;
解答 解:(1)粒子在磁场中做匀速圆周运动,设运动半径为R,
根据洛伦兹力提供向心力可得:qv0B=m$\frac{{v}_{0}^{2}}{R}$…①
由几何关系可得:xoP=2Rsin37°…②
联立①②式解得:xoP=$\frac{6m{v}_{0}}{5qB}$…③
则P点坐标为:($\frac{6m{v}_{0}}{5qB}$,0)
(2)粒子在电场中做类平抛运动,根据类平抛运动的规律得:
xoPcos37°=v0t…④
xoPsin37°=$\frac{1}{2}$at2…⑤
Eq=ma…⑥
联立③④⑤⑥式解得:E=$\frac{25}{16}B{v}_{0}$
答:(1)P点坐标为($\frac{6m{v}_{0}}{5qB}$,0);
(2)匀强电场的电场强度为$\frac{25}{16}B{v}_{0}$.
点评 本题考查带电粒子在磁场和电场中的运动,磁场中粒子做匀速圆周运动,电场中粒子做类平抛运动,解题关键是要画出粒子运动轨迹的示意图,明确粒子的运动形式,选择合适的规律解题,问题都较为常规,难度不大.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
16.一个质量为0.3kg的弹性小球,在光滑水平面上以4m/s的速度垂直撞到墙上,碰撞后小球沿相反方向运动,反弹后的速度大小与碰撞前相同.则碰撞前后小球速度变化量的大小△v和动能变化量大小△Ek为( )
| A. | △v=0,△Ek=0 | B. | △v=8m/s,△Ek=0 | ||
| C. | △v=8m/s,△Ek=4.8J | D. | △v=0,△Ek=4.8J |
6. 如图所示,单匝线圈ABCD在外力作用下以速度v向右匀速进入匀强磁场,第二次又以速度2v匀速进入同一匀强磁场.则:第二次与第一次进入时( )
如图所示,单匝线圈ABCD在外力作用下以速度v向右匀速进入匀强磁场,第二次又以速度2v匀速进入同一匀强磁场.则:第二次与第一次进入时( )
 如图所示,单匝线圈ABCD在外力作用下以速度v向右匀速进入匀强磁场,第二次又以速度2v匀速进入同一匀强磁场.则:第二次与第一次进入时( )
如图所示,单匝线圈ABCD在外力作用下以速度v向右匀速进入匀强磁场,第二次又以速度2v匀速进入同一匀强磁场.则:第二次与第一次进入时( )| A. | 线圈中电流之比为2:1 | B. | 外力做功的功率之比为4:1 | ||
| C. | 线圈中产生热量之比为4:1 | D. | 通过导线横截面电荷量之比为2:1 |
3. 如图所示,两块相同的金属板正对着竖直放置,板长为L,板间距离为d.当两板间加电压U时,一个质量为m、电荷量为+q的带电粒子,以竖直速度v0从A点射人电场,经过一段时间后从B点射出电场,不计重力影响. 则( )
如图所示,两块相同的金属板正对着竖直放置,板长为L,板间距离为d.当两板间加电压U时,一个质量为m、电荷量为+q的带电粒子,以竖直速度v0从A点射人电场,经过一段时间后从B点射出电场,不计重力影响. 则( )
 如图所示,两块相同的金属板正对着竖直放置,板长为L,板间距离为d.当两板间加电压U时,一个质量为m、电荷量为+q的带电粒子,以竖直速度v0从A点射人电场,经过一段时间后从B点射出电场,不计重力影响. 则( )
如图所示,两块相同的金属板正对着竖直放置,板长为L,板间距离为d.当两板间加电压U时,一个质量为m、电荷量为+q的带电粒子,以竖直速度v0从A点射人电场,经过一段时间后从B点射出电场,不计重力影响. 则( )| A. | 带电粒子从A点运动到B点经历的时间为$\frac{L}{{v}_{0}}$ | |
| B. | 带电粒子经过B点时速度的大小$\frac{qUL}{md{v}_{0}}$ | |
| C. | A、B两点间的电势差$\frac{{q}^{2}{U}^{2}{L}^{2}}{2m{d}^{2}{{v}_{0}}^{2}}$ | |
| D. | 带电粒子从A点运动到B点,电势能减少$\frac{{q}^{2}{U}^{2}{L}^{2}}{2m{d}^{2}{{v}_{0}}^{2}}$ |
20.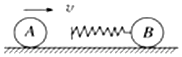 如图所示,在光滑的水平面上放有两个小球A和B其质量mA<mB,B球上固定一轻质弹簧.若将A球以速率v去碰撞静止的B球,碰撞时能量损失不计,下列说法中正确的是( )
如图所示,在光滑的水平面上放有两个小球A和B其质量mA<mB,B球上固定一轻质弹簧.若将A球以速率v去碰撞静止的B球,碰撞时能量损失不计,下列说法中正确的是( )
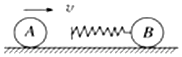 如图所示,在光滑的水平面上放有两个小球A和B其质量mA<mB,B球上固定一轻质弹簧.若将A球以速率v去碰撞静止的B球,碰撞时能量损失不计,下列说法中正确的是( )
如图所示,在光滑的水平面上放有两个小球A和B其质量mA<mB,B球上固定一轻质弹簧.若将A球以速率v去碰撞静止的B球,碰撞时能量损失不计,下列说法中正确的是( )| A. | 当弹簧压缩量最大时,A球速率最小,B球速率最大 | |
| B. | 当弹簧恢复原长时,B球速率最大 | |
| C. | 当A球速率为零时,B球速率最大 | |
| D. | 当B球速率最大时,弹性势能不为零 |
 如图所示,一足够大的倾角θ=30°的粗糙斜面上有一个粗细均匀的由同种材料制成的金属线框abcd,线框的质量m=0.6kg,其电阻值R=1.0Ω,ab边长L1=1m,bc边长L2=2m,与斜面之间的动摩擦因数μ=$\frac{{\sqrt{3}}}{9}$.斜面以EF为界,EF上侧有垂直于斜面向上的匀强磁场.一物体通过绝缘细线跨过光滑定滑轮与线框相连,连接线框的细线与斜面平行且线最初处于松弛状态.现先释放线框再释放物体,当cd边离开磁场时线框即以v=2m/s的速度匀速下滑,在ab边运动到EF位置时,细线恰好被拉直绷紧(极短时间内线框速度变化且反向),随即物体和线框一起匀速运动t=2s后开始做匀加速运动.取g=10m/s2,求:
如图所示,一足够大的倾角θ=30°的粗糙斜面上有一个粗细均匀的由同种材料制成的金属线框abcd,线框的质量m=0.6kg,其电阻值R=1.0Ω,ab边长L1=1m,bc边长L2=2m,与斜面之间的动摩擦因数μ=$\frac{{\sqrt{3}}}{9}$.斜面以EF为界,EF上侧有垂直于斜面向上的匀强磁场.一物体通过绝缘细线跨过光滑定滑轮与线框相连,连接线框的细线与斜面平行且线最初处于松弛状态.现先释放线框再释放物体,当cd边离开磁场时线框即以v=2m/s的速度匀速下滑,在ab边运动到EF位置时,细线恰好被拉直绷紧(极短时间内线框速度变化且反向),随即物体和线框一起匀速运动t=2s后开始做匀加速运动.取g=10m/s2,求:
 在原子核物理中,研究核子与核子关联的最有效途径是“双电荷交换反应”.这类反应的前半部分过程和下述力学模型类似.两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态.在它们左边有一垂直于轨道的固定挡板P,右边有一小球C沿轨道以速度v0射向B球,如图所示.C与B发生碰撞并立即结成一个整体D.在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变.然后,A球与挡板P发生碰撞,碰后A、D都静止不动,A与P接触而不粘连.过一段时间,突然解除锁定(锁定及解除锁定均无机械能损失).已知A球的质量为3m、B、C球的质量均为m.求:
在原子核物理中,研究核子与核子关联的最有效途径是“双电荷交换反应”.这类反应的前半部分过程和下述力学模型类似.两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态.在它们左边有一垂直于轨道的固定挡板P,右边有一小球C沿轨道以速度v0射向B球,如图所示.C与B发生碰撞并立即结成一个整体D.在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变.然后,A球与挡板P发生碰撞,碰后A、D都静止不动,A与P接触而不粘连.过一段时间,突然解除锁定(锁定及解除锁定均无机械能损失).已知A球的质量为3m、B、C球的质量均为m.求: 如图所示,足够长的金属导轨MN,PQ平行地固定在同一水平面上,两导轨间距L=0.20m,电阻R=0.40Ω,导轨上停放一质量m=0.10kg的金属杆ab,位于两导轨之间的金属杆的电阻r=0.10Ω,导轨的电阻可忽略不计.金属杆与导轨间的动摩擦因数为μ=0.10,整个装置处于磁感应强度B=0.50T的匀强磁场中,磁场方向竖直向下.现用一水平外力F水平向右拉金属杆,使之由静止开始运动,在整个运动过程中金属杆始终与导轨垂直并接触良好,若取国际单位,理想电压表的示数U随时间变化的数值关系为U=0.08t,从金属杆开始运动经t=5.0s时,求:
如图所示,足够长的金属导轨MN,PQ平行地固定在同一水平面上,两导轨间距L=0.20m,电阻R=0.40Ω,导轨上停放一质量m=0.10kg的金属杆ab,位于两导轨之间的金属杆的电阻r=0.10Ω,导轨的电阻可忽略不计.金属杆与导轨间的动摩擦因数为μ=0.10,整个装置处于磁感应强度B=0.50T的匀强磁场中,磁场方向竖直向下.现用一水平外力F水平向右拉金属杆,使之由静止开始运动,在整个运动过程中金属杆始终与导轨垂直并接触良好,若取国际单位,理想电压表的示数U随时间变化的数值关系为U=0.08t,从金属杆开始运动经t=5.0s时,求: