题目内容
20．
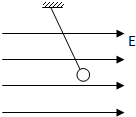如图所示，悬线下挂着一个带正电的小球，它的质量为m，电荷量为q，整个装置处于水平向右的匀强电场中，电场强度为E，下列说法正确的是（ ）| A． | 小球平衡时，悬线与竖直方向夹角的正弦值为$\frac{qE}{mg}$ | |
| B． | 若剪断悬线，则小球做匀加速直线运动 | |
| C． | 若剪断悬线，则小球做曲线运动 | |
| D． | 若剪断悬线，则小球做匀速运动 |
分析 小球受重力、电场力和拉力作用下处于平衡，根据共点力平衡求出悬线与竖直方向夹角的正切值； 剪断细线，根据小球的受力和初速度判断其运动情况．
解答 
解：A、小球受到重力、电场力和拉力处于平衡，根据共点力平衡得，mgtanθ=qE，则tanθ=$\frac{qE}{mg}$．故A错误．
BCD、剪断细线后，小球受重力和电场力，这两个力都是恒力，则其合力为恒力．合力的方向与原来绳子的拉力方向等值反向，所以小球沿细绳方向做初速度为零的匀加速直线运动．故B正确，CD错误．
故选：B
点评 本题考查带电粒子在电场中的运动问题，要注意正确分析受力，明确平衡条件的应用以及牛顿第二定律的应用，知道小球由静止开始在恒力作用下的运动一定是匀加速直线运动．
练习册系列答案
阅读快车系列答案
相关题目
3．
在台秤上，框架内有一轻弹簧，其上端固定在框架顶部，下端系一质量为m的物体，物体下方用竖直细线与框架下部固定，各物体都处于静止状态．今剪断细线，物体开始振动，且框架始终没有离开台秤，弹簧不超出弹性限度，空气阻力忽略不计，重力加速度为g．则下列说法正确的是（ ）
在台秤上，框架内有一轻弹簧，其上端固定在框架顶部，下端系一质量为m的物体，物体下方用竖直细线与框架下部固定，各物体都处于静止状态．今剪断细线，物体开始振动，且框架始终没有离开台秤，弹簧不超出弹性限度，空气阻力忽略不计，重力加速度为g．则下列说法正确的是（ ）| A． | 当台秤示数最小时弹簧的长度一定最短 | |
| B． | 当台秤示数最小时物体一定处在平衡位置 | |
| C． | 振动过程中台秤的最大示数一定大于（M+m）g | |
| D． | 振动过程中台秤的最大示数一定等于（M+m）g |
11．如图，一块足够长的浅色长木板，静止地放置在水平地面上．一个煤块静止在该木板上，煤块与木板间的滑动摩擦系数为μ．突然，使木板以恒定的速度v0做匀速直线运动，煤块将在木板上划下黑色痕迹．经过某一时间t，令木板突然停下，以后不再运动．已知重力加速度为g，煤块可视为质点，不计煤块与木板摩擦中损失的质量．则在最后煤块不再运动时，木板上出现的黑色痕迹的长度可能是（ ）
| A． | $\frac{v_0^2}{2μg}$ | B． | v0 t | C． | v0t-$\frac{1}{2}$μgt2 | D． | $\frac{v_0^2}{μg}$ |
8．
如图所示，一倾角θ=37°的足够长斜面固定在水平地面上．当t=0时，滑块以初速度v0=10m/s沿斜面向上运动，已知滑块与斜面间的动摩擦因数μ=0.5，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8．下列说法正确的是（ ）
如图所示，一倾角θ=37°的足够长斜面固定在水平地面上．当t=0时，滑块以初速度v0=10m/s沿斜面向上运动，已知滑块与斜面间的动摩擦因数μ=0.5，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8．下列说法正确的是（ ）| A． | 滑块一直做匀变速直线运动 | |
| B． | t=1s时，滑块速度减为零，然后静止在斜面上 | |
| C． | t=2s时，滑块恰好又回到出发点 | |
| D． | t=3s时，滑块的速度为4m/s |
15．
战斗机水平飞行时，飞行员从左侧舷窗看到如图甲所示的“天地分界线”．当飞行员从左侧舷窗看到的“天地分界线”如图乙所示时，飞机可能正在（ ）
战斗机水平飞行时，飞行员从左侧舷窗看到如图甲所示的“天地分界线”．当飞行员从左侧舷窗看到的“天地分界线”如图乙所示时，飞机可能正在（ ）| A． | 斜向上爬升 | B． | 斜向下俯冲 | C． | 竖直向上爬升 | D． | 竖直向下俯冲 |
2016年新春佳节，我市的许多餐厅生意火爆，常常人满为患，为能服务更多的顾客，服务员需要用最短的时间将菜肴送至顾客处（设菜品送到顾客处速度恰好为零）．某次服务员用单手托托盘方式（如图）给12m远处的顾客上菜，要求全程托盘水平．托盘和手、碗之间的摩擦因数分别为0.2、0.15，服务员上菜最大速度为3m/s．假设服务员加速、减速运动过程中是匀变速直线运动，且可认为最大静摩擦力等于滑动摩擦力．则：
12．
如图所示，在光滑水平面上有一根弹簧固定在墙上，一木块以速度v向右运动，从木块与弹簧接触到弹簧被压缩成最短的过程中，木块所做的运动是（ ）
如图所示，在光滑水平面上有一根弹簧固定在墙上，一木块以速度v向右运动，从木块与弹簧接触到弹簧被压缩成最短的过程中，木块所做的运动是（ ）| A． | 加速度增大的变减速运动 | B． | 匀减速运动 | ||
| C． | 加速度减小的变减速运动 | D． | 无法确定 |
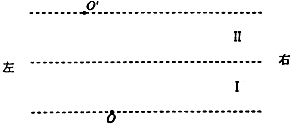如图所示，真空中区域I和区域Ⅱ内存在着与纸面垂直的方向相反的匀强磁场，磁感应强度大小均为B．在区域II的上边界线上的N点固定一负的点电荷，并采取措施使之只对区域II以上空间产生影响．一带正电的粒子质量为m，电荷量为q，自区域I下边界线上的O点以速度v0垂直于磁场边界及磁场方向射入磁场，经过一段时间粒子通过区域Ⅱ边界上的O'点，最终又从区域I下边界上的P点射出．图中N、P两点均未画出，但已知N点在O′点的右方，且N点与O′点相距L．区域I和Ⅱ的宽度为d=$\frac{m{v}_{0}}{2qB}$，两区域的长度足够大．N点的负电荷所带电荷量的绝对值为Q=$\frac{Lm{v}_{0}^{2}}{kq}$（其中k为静电力常量）．不计粒子的重力，求：
如图，光滑斜面PMNQ的倾角为θ，斜面上放置一矩形导体线框abcd，其中ab边长为l1，bc边长为l2，线框质量为m，电阻为R，有界匀强磁场的磁感应强度为B，方向垂直于斜面向上，ef为磁场的边界，且ef∥MN．线框在恒力F作用下从静止开始运动，其ab边始终保持与底边MN平行，F沿斜面向上且与斜面平行，已知线框刚进入磁场时做匀速运动，则线框进入磁场时的速度为$\frac{（F-mgsinθ）R}{{B}_{\;}^{2}{l}_{1}^{2}}$．线框进入磁场的过程中产生的热量为$（F-mgsinθ）•{l}_{2}^{\;}$．