题目内容
10. 如图,光滑斜面PMNQ的倾角为θ,斜面上放置一矩形导体线框abcd,其中ab边长为l1,bc边长为l2,线框质量为m,电阻为R,有界匀强磁场的磁感应强度为B,方向垂直于斜面向上,ef为磁场的边界,且ef∥MN.线框在恒力F作用下从静止开始运动,其ab边始终保持与底边MN平行,F沿斜面向上且与斜面平行,已知线框刚进入磁场时做匀速运动,则线框进入磁场时的速度为$\frac{(F-mgsinθ)R}{{B}_{\;}^{2}{l}_{1}^{2}}$.线框进入磁场的过程中产生的热量为$(F-mgsinθ)•{l}_{2}^{\;}$.
如图,光滑斜面PMNQ的倾角为θ,斜面上放置一矩形导体线框abcd,其中ab边长为l1,bc边长为l2,线框质量为m,电阻为R,有界匀强磁场的磁感应强度为B,方向垂直于斜面向上,ef为磁场的边界,且ef∥MN.线框在恒力F作用下从静止开始运动,其ab边始终保持与底边MN平行,F沿斜面向上且与斜面平行,已知线框刚进入磁场时做匀速运动,则线框进入磁场时的速度为$\frac{(F-mgsinθ)R}{{B}_{\;}^{2}{l}_{1}^{2}}$.线框进入磁场的过程中产生的热量为$(F-mgsinθ)•{l}_{2}^{\;}$.
分析 根据题意,线框刚进入磁场做匀速运动,根据受力平衡即可求出线框进入磁场时的速度,线框进入磁场过程中产生的热量等于克服安培力做的功.
解答 解:设线框进入磁场时的速度为v
刚进入磁场时,感应电动势E=$B{l}_{1}^{\;}v$
感应电流$I=\frac{E}{R}=\frac{B{l}_{1}^{\;}v}{R}$
安培力${F}_{安}^{\;}=BI{l}_{1}^{\;}=B\frac{B{l}_{1}^{\;}v}{R}{l}_{1}^{\;}=\frac{{B}_{\;}^{2}{l}_{1}^{2}v}{R}$
线框匀速进入磁场,受力平衡,则有
$F=mgsinθ+{F}_{安}^{\;}$
代入:$F=mgsinθ+\frac{{B}_{\;}^{2}{l}_{1}^{2}v}{R}$
解得:$v=\frac{(F-mgsinθ)R}{{B}_{\;}^{2}{l}_{1}^{2}}$
线框进入磁场过程中产生的焦耳热等于克服安培力做的功
Q=${W}_{克安}^{\;}={F}_{安}^{\;}•{l}_{2}^{\;}$=$(F-mgsinθ)•{l}_{2}^{\;}$
故答案为:$\frac{(F-mgsinθ)R}{{B}_{\;}^{2}{l}_{1}^{2}}$ $(F-mgsinθ)•{l}_{2}^{\;}$
点评 本题首先要正确分析线框的运动情况,会推导安培力的表达式,把握能量是如何转化的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.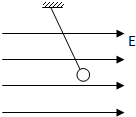 如图所示,悬线下挂着一个带正电的小球,它的质量为m,电荷量为q,整个装置处于水平向右的匀强电场中,电场强度为E,下列说法正确的是( )
如图所示,悬线下挂着一个带正电的小球,它的质量为m,电荷量为q,整个装置处于水平向右的匀强电场中,电场强度为E,下列说法正确的是( )
 如图所示,悬线下挂着一个带正电的小球,它的质量为m,电荷量为q,整个装置处于水平向右的匀强电场中,电场强度为E,下列说法正确的是( )
如图所示,悬线下挂着一个带正电的小球,它的质量为m,电荷量为q,整个装置处于水平向右的匀强电场中,电场强度为E,下列说法正确的是( )| A. | 小球平衡时,悬线与竖直方向夹角的正弦值为$\frac{qE}{mg}$ | |
| B. | 若剪断悬线,则小球做匀加速直线运动 | |
| C. | 若剪断悬线,则小球做曲线运动 | |
| D. | 若剪断悬线,则小球做匀速运动 |
5.如图1所示,有一厚度均匀质量M=2kg的木板A在水平桌面上始终向右匀速运动,木板与桌面的动摩擦因数为μ=0.1,t=0时刻把一质量为m=1kg的物体B以一定水平初速度放在木板A的右端,B在A上的位移s随时间t变化关系如图2所示(图象前3s内为抛物线,3s~4.5s内为直线,取向左运动的方向为正方向)g=10m/s2,下列说法正确的是( )


| A. | 木板的速度大小为2m/s | |
| B. | 3s~4.5s时间内,物体B的加速度大小为2m/s2 | |
| C. | AB间的动摩擦因数为0.2 | |
| D. | 0~2s为保持木板做匀速运动,需施加一个水平向右大小为3N的力 |
2. 如图所示,带箭头的线表示某一电场的电场线.在电场力作用下,一带电粒子(不计重力)经A点飞向B点,轨迹如图.正确的是( )
如图所示,带箭头的线表示某一电场的电场线.在电场力作用下,一带电粒子(不计重力)经A点飞向B点,轨迹如图.正确的是( )
 如图所示,带箭头的线表示某一电场的电场线.在电场力作用下,一带电粒子(不计重力)经A点飞向B点,轨迹如图.正确的是( )
如图所示,带箭头的线表示某一电场的电场线.在电场力作用下,一带电粒子(不计重力)经A点飞向B点,轨迹如图.正确的是( )| A. | 粒子带负电 | B. | 粒子在A点加速度小 | ||
| C. | 粒子在B点动能大 | D. | A、B两点相比,A点电势较低 |
19.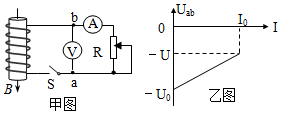 如甲图所示,n匝面积为S的线圈处在竖直向下的匀强磁场中,该磁场的磁感应强度随时间均匀变化.S闭合后,移动滑动变阻器的滑片,测出多组U、I值,描出电源两端电压随电流I变化的图象如乙图.下列说法正确的是( )
如甲图所示,n匝面积为S的线圈处在竖直向下的匀强磁场中,该磁场的磁感应强度随时间均匀变化.S闭合后,移动滑动变阻器的滑片,测出多组U、I值,描出电源两端电压随电流I变化的图象如乙图.下列说法正确的是( )
 如甲图所示,n匝面积为S的线圈处在竖直向下的匀强磁场中,该磁场的磁感应强度随时间均匀变化.S闭合后,移动滑动变阻器的滑片,测出多组U、I值,描出电源两端电压随电流I变化的图象如乙图.下列说法正确的是( )
如甲图所示,n匝面积为S的线圈处在竖直向下的匀强磁场中,该磁场的磁感应强度随时间均匀变化.S闭合后,移动滑动变阻器的滑片,测出多组U、I值,描出电源两端电压随电流I变化的图象如乙图.下列说法正确的是( )| A. | 磁场均匀减小,磁场变化率$\frac{△B}{△t}$=$\frac{U}{nS}$,线圈的电阻r=$\frac{{U}_{0}}{{I}_{0}}$ | |
| B. | 磁场均匀减小,磁场变化率$\frac{△B}{△t}$=$\frac{{U}_{0}}{nS}$,线圈的电阻r=$\frac{{U}_{0}-U}{{I}_{0}}$ | |
| C. | 磁场均匀增大,磁场变化率$\frac{△B}{△t}$=$\frac{U}{nS}$,线圈的电阻r=$\frac{{U}_{0}}{{I}_{0}}$ | |
| D. | 磁场均匀增大,磁场变化率$\frac{△B}{△t}$=$\frac{{U}_{0}}{nS}$,线圈的电阻r=$\frac{{U}_{0}-U}{{I}_{0}}$ |
 某次对新能源汽车性能进行的测量中,汽车在水平测试平台上由静止开始沿直线运动,汽车所受动力随时间变化关系如图1所示,而速度传感器只传回第10s以后的数据(如图2所示).已知汽车质量为1000kg,汽车所受阻力恒定.求:
某次对新能源汽车性能进行的测量中,汽车在水平测试平台上由静止开始沿直线运动,汽车所受动力随时间变化关系如图1所示,而速度传感器只传回第10s以后的数据(如图2所示).已知汽车质量为1000kg,汽车所受阻力恒定.求: 如图所示,线圈面积S=1×10-3m2,匝数n=100,两端点连接一电容器,其电容C=30 μF.线圈中磁场的磁感应强度按$\frac{△B}{△t}$=0.1T/s增加,磁场方向垂直线圈平面向里,那么电容器所带电荷量为$3×1{0}_{\;}^{-7}C$电容器的极板a带正电(填“正”或“负”).
如图所示,线圈面积S=1×10-3m2,匝数n=100,两端点连接一电容器,其电容C=30 μF.线圈中磁场的磁感应强度按$\frac{△B}{△t}$=0.1T/s增加,磁场方向垂直线圈平面向里,那么电容器所带电荷量为$3×1{0}_{\;}^{-7}C$电容器的极板a带正电(填“正”或“负”). 某同学想测出济南当地的重力加速度g,并验证机械能守恒定律.为了减小误差,他设计了一个实验如下:将一根长直铝棒用细线悬挂在空中(如图甲所示),在靠近铝棒下端的一侧固定电动机M,使电动机转轴处于竖直方向,在转轴上水平固定一支特制笔N,借助转动时的现象,将墨汁甩出形成一条细线.调整笔的位置,使墨汁在棒上能清晰地留下墨线.启动电动机待转速稳定后,用火烧断悬线,让铝棒自由下落,笔在铝棒上相应位置留下墨线.图乙是实验时在铝棒上所留下的墨线,将某条合适的墨线A作为起始线,此后每隔4条墨线取一条计数墨线,分别记作B、C、D、E.将最小刻度为毫米的刻度尺的零刻度线对准A,此时B、C、D、E对应的刻度依次为14.68cm、39.15cm、73.41cm、117.46cm.已知电动机的转速为3000r/min.求:
某同学想测出济南当地的重力加速度g,并验证机械能守恒定律.为了减小误差,他设计了一个实验如下:将一根长直铝棒用细线悬挂在空中(如图甲所示),在靠近铝棒下端的一侧固定电动机M,使电动机转轴处于竖直方向,在转轴上水平固定一支特制笔N,借助转动时的现象,将墨汁甩出形成一条细线.调整笔的位置,使墨汁在棒上能清晰地留下墨线.启动电动机待转速稳定后,用火烧断悬线,让铝棒自由下落,笔在铝棒上相应位置留下墨线.图乙是实验时在铝棒上所留下的墨线,将某条合适的墨线A作为起始线,此后每隔4条墨线取一条计数墨线,分别记作B、C、D、E.将最小刻度为毫米的刻度尺的零刻度线对准A,此时B、C、D、E对应的刻度依次为14.68cm、39.15cm、73.41cm、117.46cm.已知电动机的转速为3000r/min.求: 如图所示,在xOy平面内,x=2L处竖直放置一个长为L的粒子吸收板AB,其下端点A在x轴上,粒子打到吸收板上立即被板吸收,不考虑吸收板带电对粒子运动的影响.在AB左侧存在竖直向上的匀强电场,场强大小为E,在AB右侧存在垂直存在垂直纸面向外的匀强磁场.原点O处有一粒子源,可沿x轴正向射出质量为m、电量为+q的不同速率的带电粒子,不计粒子的重力.
如图所示,在xOy平面内,x=2L处竖直放置一个长为L的粒子吸收板AB,其下端点A在x轴上,粒子打到吸收板上立即被板吸收,不考虑吸收板带电对粒子运动的影响.在AB左侧存在竖直向上的匀强电场,场强大小为E,在AB右侧存在垂直存在垂直纸面向外的匀强磁场.原点O处有一粒子源,可沿x轴正向射出质量为m、电量为+q的不同速率的带电粒子,不计粒子的重力.