��Ŀ����
9��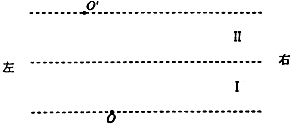 ��ͼ��ʾ�����������I��������ڴ�������ֽ�洹ֱ�ķ����෴����ǿ�ų����Ÿ�Ӧǿ�ȴ�С��ΪB��������II���ϱ߽����ϵ�N��̶�һ���ĵ��ɣ�����ȡ��ʩʹֻ֮������II���Ͽռ����Ӱ�죮һ���������������Ϊm�������Ϊq��������I�±߽����ϵ�O�����ٶ�v0��ֱ�ڴų��߽缰�ų���������ų�������һ��ʱ������ͨ�������߽��ϵ�O'�㣬�����ִ�����I�±߽��ϵ�P�������ͼ��N��P�����δ����������֪N����O�����ҷ�����N����O������L������I�͢�Ŀ���Ϊd=$\frac{m{v}_{0}}{2qB}$��������ij����㹻��N��ĸ��������������ľ���ֵΪQ=$\frac{Lm{v}_{0}^{2}}{kq}$������kΪ���������������������ӵ���������
��ͼ��ʾ�����������I��������ڴ�������ֽ�洹ֱ�ķ����෴����ǿ�ų����Ÿ�Ӧǿ�ȴ�С��ΪB��������II���ϱ߽����ϵ�N��̶�һ���ĵ��ɣ�����ȡ��ʩʹֻ֮������II���Ͽռ����Ӱ�죮һ���������������Ϊm�������Ϊq��������I�±߽����ϵ�O�����ٶ�v0��ֱ�ڴų��߽缰�ų���������ų�������һ��ʱ������ͨ�������߽��ϵ�O'�㣬�����ִ�����I�±߽��ϵ�P�������ͼ��N��P�����δ����������֪N����O�����ҷ�����N����O������L������I�͢�Ŀ���Ϊd=$\frac{m{v}_{0}}{2qB}$��������ij����㹻��N��ĸ��������������ľ���ֵΪQ=$\frac{Lm{v}_{0}^{2}}{kq}$������kΪ���������������������ӵ�����������1�������ڴų�����Բ���˶��Ĺ���뾶��
��2��������O��O��֮���˶��켣�ij��Ⱥ�λ�ƵĴ�С��
��3�����Ӵ�O�㵽P�����õ�ʱ�估O��P�����ľ��룮
���� ��1�������������ṩ����������ð뾶��ʽ��
��2�����������͢�ų��Ĵ�С��ȷ����෴�����Դ�O�㴹ֱ���������������Բ���˶��ķ����෴���˶��켣���жԳ��ԣ�������֪�ų�����d�ı���ʽ���Կ����뾶�����d�����ɼ��ι�ϵ��ϵ�ҵ������������ų�������ƫת�ĽǶȣ��Ӷ������·�̺�λ�ƣ�
��3���ɷ���֪������ɴ�ֱ���������ϱ߽羭��O��㣬���븺���Ӳ����ĵ糡��ֱ��������ܵ��Ŀ�����Ϊ$F=\frac{kQq}{{l}^{2}}=\frac{m{{v}_{0}}^{2}}{l}$����������ɽ���N��������Բ���˶���ת����Ȧ���ٴλص��������ϱ�Ե����������͢����ֱ�������Բ���˶������˶��ĶԳ��Ժ���ؼ��ι�ϵ����������Ӵ�O�㵽P�����õ�ʱ�估O��P�����ľ��룮
��� �⣺��1����$qB{v}_{0}=\frac{m{{v}_{0}}^{2}}{R}$�ù���뾶Ϊ��$R=\frac{m{v}_{0}}{qB}$
��2��������֪��R=2d��
���������ڴų���ƫת�Ƕȣ�$��=30��=\frac{��}{6}$
�˶��켣�ij��ȣ�$s=2R��=\frac{��m{v}_{0}}{3qB}$
λ�ƵĴ�С��x=4Rsin15��=4Rsin��45��-30�㣩=$\frac{��\sqrt{6}-\sqrt{2}��m{v}_{0}}{qB}$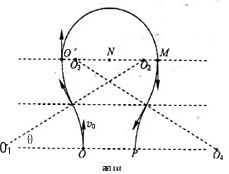
��3���ɷ���֪������ɴ�ֱ���������ϱ߽羭��O��㣬���븺���Ӳ����ĵ糡��
ֱ��������ܵ��Ŀ�����Ϊ$F=\frac{kQq}{{L}^{2}}=\frac{m{{v}_{0}}^{2}}{L}$����������ɽ���N��������Բ���˶���
�ڴų����˶����ڣ�${T}_{1}=\frac{2��m}{qB}$
�ڴų����˶���Ӧ���ܽǶȣ�$��=4��=\frac{2��}{3}$
�ڴų����˶�����ʱ�䣺${t}_{1}=\frac{��}{2��}{T}_{1}=\frac{2��m}{3qB}$
�ڵ糡���˶����ڣ�${T}_{2}=\frac{2��L}{{v}_{0}}$
�ڵ糡���˶�ʱ�䣺${t}_{2}=\frac{{T}_{2}}{2}=\frac{��L}{{v}_{0}}$
����ɴ�O�㵽P���ʱ�䣺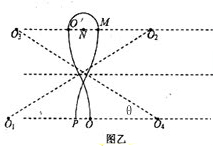 $t={t}_{1}+{t}_{2}=\frac{2��m}{3qB}+\frac{��L}{{v}_{0}}$
$t={t}_{1}+{t}_{2}=\frac{2��m}{3qB}+\frac{��L}{{v}_{0}}$
����ɴ�O�㵽O���Ĺ�������ƽ���ڱ߽��߷���ƫ�Ƶľ��룺
${x}_{1}=2��R-Rcos30�㣩=��2-\sqrt{3}��R$
��L��x1 ʱ����ͼ����ʾ����O��P�����ľ���Ϊ��
${l}_{OP}=2��L-{x}_{1}��=2[L-\frac{��2-\sqrt{3}��m{v}_{0}}{qB}]$
��L��x1 ʱ����ͼ����ʾ����O��P����ľ���Ϊ��
${l}_{OP}=2��{x}_{1}-L��=2[\frac{��2-\sqrt{3}��m{v}_{0}}{qB}-L]$
�𣺣�1�������ڴų�����Բ���˶��Ĺ���뾶$\frac{m{v}_{0}}{qB}$��
��2��������O��O��֮���˶��켣�ij���Ϊ$\frac{��m{v}_{0}}{3qB}$��λ�ƵĴ�С$\frac{��\sqrt{6}-\sqrt{2}��m{v}_{0}}{qB}$��
��3�����Ӵ�O�㵽P�����õ�ʱ��Ϊ$\frac{2��m}{3qB}+\frac{��L}{{v}_{0}}$��O��P�����ľ��룺
�ٵ�L��x1 ʱ��O��P�����ľ���Ϊ��${l}_{OP}=2��L-{x}_{1}��=2[L-\frac{��2-\sqrt{3}��m{v}_{0}}{qB}]$��
�ڵ�L��x1 ʱ��O��P����ľ���Ϊ��${l}_{OP}=2��{x}_{1}-L��=2[\frac{��2-\sqrt{3}��m{v}_{0}}{qB}-L]$��
���� ������������ڣ��������ڢ��˶�������Բ���˶�����ת�������෴�����Ծ��жԳ��ԣ����й�ϵR=2d����Ϊ���������ṩ���㣮������N��ĸ��������������ľ���ֵΪ$Q=\frac{Lm{{v}_{0}}^{2}}{kq}$����q��Q֮��Ŀ�����$F=\frac{kQq}{{L}^{2}}=\frac{m{{v}_{0}}^{2}}{L}$���պ�ʹq��N�����뾶ΪL������Բ���˶������������˶��켣�ͷdz��Գƣ�ʱ�����������������

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д�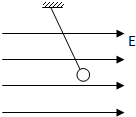 ��ͼ��ʾ�������¹���һ���������С����������Ϊm�������Ϊq������װ�ô���ˮƽ���ҵ���ǿ�糡�У��糡ǿ��ΪE������˵����ȷ���ǣ�������
��ͼ��ʾ�������¹���һ���������С����������Ϊm�������Ϊq������װ�ô���ˮƽ���ҵ���ǿ�糡�У��糡ǿ��ΪE������˵����ȷ���ǣ�������| A�� | С��ƽ��ʱ����������ֱ����нǵ�����ֵΪ$\frac{qE}{mg}$ | |
| B�� | ���������ߣ���С�����ȼ���ֱ���˶� | |
| C�� | ���������ߣ���С���������˶� | |
| D�� | ���������ߣ���С���������˶� |
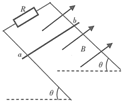 ��ͼ��ʾ�����ΪL���㹻���Ĺ⻬������б���ã���ˮƽ�����Ϊ�ȣ����϶�����һ����ֵ����R����ǿ�ų��Ÿ�Ӧǿ��ΪB������ֱ�ڵ�������ƽ�棬������Ϊm�Ľ�����ab�ڵ��������ٶ��ͷţ���ab���»����ȶ�״̬ʱ������R�ĵ繦��ΪP������ͽ������ĵ�������ƣ��������ٶ�Ϊg�������ж���ȷ���ǣ�������
��ͼ��ʾ�����ΪL���㹻���Ĺ⻬������б���ã���ˮƽ�����Ϊ�ȣ����϶�����һ����ֵ����R����ǿ�ų��Ÿ�Ӧǿ��ΪB������ֱ�ڵ�������ƽ�棬������Ϊm�Ľ�����ab�ڵ��������ٶ��ͷţ���ab���»����ȶ�״̬ʱ������R�ĵ繦��ΪP������ͽ������ĵ�������ƣ��������ٶ�Ϊg�������ж���ȷ���ǣ�������| A�� | �������a�˵��Ʊ�b�˵��Ƹ� | |
| B�� | ab���ڴﵽ�ȶ�״̬ǰ�����ٶ����ӵļ����˶� | |
| C�� | ab���»����ȶ�״̬ʱ�����������ٶ�v=$\frac{mgRsin��}{{B}^{2}{L}^{2}}$ | |
| D�� | ������һ������Ϊԭ��2���ĵ�����������������䣬��ab���»����ȶ�״̬ʱ������R�ĵ繦�ʽ���Ϊԭ����2�� |
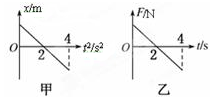 ����ס���ԭ����ֹ�ڹ⻬ˮƽ���ϣ���t=0ʱ�̿�ʼ������ˮƽ����ֱ���˶���λ��x��ʱ��ƽ��t2�Ĺ�ϵͼ����ͼ�ף����ܵ���ͼ����ʾ��ˮƽ����F�����ã�����0��4s��ʱ���ڣ�������
����ס���ԭ����ֹ�ڹ⻬ˮƽ���ϣ���t=0ʱ�̿�ʼ������ˮƽ����ֱ���˶���λ��x��ʱ��ƽ��t2�Ĺ�ϵͼ����ͼ�ף����ܵ���ͼ����ʾ��ˮƽ����F�����ã�����0��4s��ʱ���ڣ�������| A�� | ���������ܺ������ϱ仯 | B�� | 2sĩ�������ٶȴﵽ��� | ||
| C�� | 2sĩ�������ٶ�Ϊ0 | D�� | 2sĩ������ı��˶����� | ||
| E�� | ��������ٶȲ��ϼ�С |
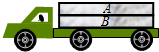 ��ͼ��ʾ����������A��B�����ڿ�����ˮƽ�װ��ϣ������װ��B�䶯Ħ������Ϊ��1��A��B�䶯Ħ������Ϊ��2����1����2������ɲ���������ٶ�Ϊa��a����1g��������Ϊ���Ħ�����뻬��Ħ������С��ȣ�������ƽֱ��·��ʻ;�������������ʱ��Ҫ����ɲ������s0�������ܰ�ȫͣ�£�����ʻ���ٶȲ��ܳ�����������
��ͼ��ʾ����������A��B�����ڿ�����ˮƽ�װ��ϣ������װ��B�䶯Ħ������Ϊ��1��A��B�䶯Ħ������Ϊ��2����1����2������ɲ���������ٶ�Ϊa��a����1g��������Ϊ���Ħ�����뻬��Ħ������С��ȣ�������ƽֱ��·��ʻ;�������������ʱ��Ҫ����ɲ������s0�������ܰ�ȫͣ�£�����ʻ���ٶȲ��ܳ�����������| A�� | $\sqrt{2a{s}_{0}}$ | B�� | $\sqrt{2{��}_{1}g{s}_{0}}$ | C�� | $\sqrt{2{��}_{2}g{s}_{0}}$ | D�� | $\sqrt{��{��}_{1}+{��}_{2}��g{s}_{0}}$ |
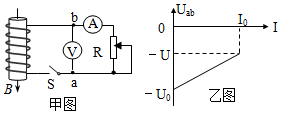 ���ͼ��ʾ��n�����ΪS����Ȧ������ֱ���µ���ǿ�ų��У��ôų��ĴŸ�Ӧǿ����ʱ����ȱ仯��S�պϺ��ƶ������������Ļ�Ƭ���������U��Iֵ�������Դ���˵�ѹ�����I�仯��ͼ������ͼ������˵����ȷ���ǣ�������
���ͼ��ʾ��n�����ΪS����Ȧ������ֱ���µ���ǿ�ų��У��ôų��ĴŸ�Ӧǿ����ʱ����ȱ仯��S�պϺ��ƶ������������Ļ�Ƭ���������U��Iֵ�������Դ���˵�ѹ�����I�仯��ͼ������ͼ������˵����ȷ���ǣ�������| A�� | �ų����ȼ�С���ų��仯��$\frac{��B}{��t}$=$\frac{U}{nS}$����Ȧ�ĵ���r=$\frac{{U}_{0}}{{I}_{0}}$ | |
| B�� | �ų����ȼ�С���ų��仯��$\frac{��B}{��t}$=$\frac{{U}_{0}}{nS}$����Ȧ�ĵ���r=$\frac{{U}_{0}-U}{{I}_{0}}$ | |
| C�� | �ų��������ų��仯��$\frac{��B}{��t}$=$\frac{U}{nS}$����Ȧ�ĵ���r=$\frac{{U}_{0}}{{I}_{0}}$ | |
| D�� | �ų��������ų��仯��$\frac{��B}{��t}$=$\frac{{U}_{0}}{nS}$����Ȧ�ĵ���r=$\frac{{U}_{0}-U}{{I}_{0}}$ |
 ij�ζ�����Դ�������ܽ��еIJ����У�������ˮƽ����ƽ̨���ɾ�ֹ��ʼ��ֱ���˶����������ܶ�����ʱ��仯��ϵ��ͼ1��ʾ�����ٶȴ�����ֻ���ص�10s�Ժ�����ݣ���ͼ2��ʾ������֪��������Ϊ1000kg���������������㶨����
ij�ζ�����Դ�������ܽ��еIJ����У�������ˮƽ����ƽ̨���ɾ�ֹ��ʼ��ֱ���˶����������ܶ�����ʱ��仯��ϵ��ͼ1��ʾ�����ٶȴ�����ֻ���ص�10s�Ժ�����ݣ���ͼ2��ʾ������֪��������Ϊ1000kg���������������㶨����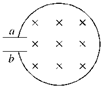 ��ͼ��ʾ����Ȧ���S=1��10-3m2������n=100�����˵�����һ�������������C=30 ��F����Ȧ�дų��ĴŸ�Ӧǿ�Ȱ�$\frac{��B}{��t}$=0.1T/s���ӣ��ų�����ֱ��Ȧƽ�������ô���������������Ϊ$3��1{0}_{\;}^{-7}C$�������ļ���a�����磨�������������
��ͼ��ʾ����Ȧ���S=1��10-3m2������n=100�����˵�����һ�������������C=30 ��F����Ȧ�дų��ĴŸ�Ӧǿ�Ȱ�$\frac{��B}{��t}$=0.1T/s���ӣ��ų�����ֱ��Ȧƽ�������ô���������������Ϊ$3��1{0}_{\;}^{-7}C$�������ļ���a�����磨�������������