题目内容
12. 在如图所示的光滑水平面上,小明站在静止的小车上用力向右推静止的木箱,木箱离开手以5m/s的速度向右匀速运动,运动一段时间后与竖直墙壁发生弹性碰撞,反弹回来后被小明接住.已知木箱的质量为30kg,人与车的质量为50kg.求:
在如图所示的光滑水平面上,小明站在静止的小车上用力向右推静止的木箱,木箱离开手以5m/s的速度向右匀速运动,运动一段时间后与竖直墙壁发生弹性碰撞,反弹回来后被小明接住.已知木箱的质量为30kg,人与车的质量为50kg.求:(1)推出木箱后小明和小车一起运动的速度大小;
(2)小明接住木箱后三者一起运动,在接木箱过程中系统损失的能量.
分析 (1)在推出木箱的过程中,木箱和小明以及车组成的系统动量守恒,根据动量守恒定律求出推出木箱后小明和小车一起运动的速度v1的大小;
(2)小明在接木箱的过程中动量守恒,根据动量守恒定律求出小明接住木箱后三者一起运动的速度v2的大小.然后由能量守恒定律求出损失的机械能.
解答 解:(1)人小明推出木箱过程系统动量守恒,取向左为正方向,由动量守恒定律得:
m1v1-m2v=0,
解得:v1=$\frac{30×5}{50}m/s=3m/s$.
(2)小明接木箱的过程中动量守恒,以向左为正方向,由动量守恒定律得:
m2v+m1v1=(m1+m2)v2,
解得:v2=$\frac{30×5+50×3}{80}m/s=3.75m/s$.
根据能量守恒得,$△E=\frac{1}{2}{m}_{1}{{v}_{1}}^{2}+\frac{1}{2}{m}_{2}{v}^{2}-$$\frac{1}{2}({m}_{1}+{m}_{2}){{v}_{2}}^{2}$,
代入数据解得△E=37.5J.
答:(1)推出木箱后小明和小车一起运动的速度大小为3m/s;
(2)小明接住木箱后三者一起运动,在接木箱过程中系统损失的能量为37.5J.
点评 解决本题的关键掌握动量守恒定律,以及在运用动量守恒定律解题时注意速度的方向.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
2.下列说法正确的( )
| A. | 布朗运动就是液体分子的热运动 | |
| B. | 当分子间距离减小时,分子势能不一定减小 | |
| C. | 一定质量的理想气体在温度不变的条件下,压强增大,则外界对气体做正功 | |
| D. | 一切自然过程总是向分子热运动的无序性增大的方向进行 | |
| E. | 第二类永动机不可能制成是因为它违反了能量守恒定律 |
3. 如图所示,虚线a、b、c、d表示O处点电荷的电场中的三个等势面,设两相邻等势面间距相等,一带电粒子(不计重力)射入电场后的运动轨迹为图中实线所示,其中1、2、3、4表示运动轨迹与等势线的交点,由此可以判定( )
如图所示,虚线a、b、c、d表示O处点电荷的电场中的三个等势面,设两相邻等势面间距相等,一带电粒子(不计重力)射入电场后的运动轨迹为图中实线所示,其中1、2、3、4表示运动轨迹与等势线的交点,由此可以判定( )
 如图所示,虚线a、b、c、d表示O处点电荷的电场中的三个等势面,设两相邻等势面间距相等,一带电粒子(不计重力)射入电场后的运动轨迹为图中实线所示,其中1、2、3、4表示运动轨迹与等势线的交点,由此可以判定( )
如图所示,虚线a、b、c、d表示O处点电荷的电场中的三个等势面,设两相邻等势面间距相等,一带电粒子(不计重力)射入电场后的运动轨迹为图中实线所示,其中1、2、3、4表示运动轨迹与等势线的交点,由此可以判定( )| A. | O处的点电荷一定带负电 | |
| B. | 带电粒子在位置2电势能一定大于位置4的电势能 | |
| C. | 带电粒子从位置1到2和从位置3到4的过程中电场力做的功大小关系是W12=2W34 | |
| D. | a、b、c三个等势面的电势大小关系是φa<φb<φc |
17. 一电阻为R的金属线圈放入磁场中,穿过线圈的磁通量随时间的变化如图所示,在0-t0时间内通过线圈上某位置横截面的电荷量为q,则( )
一电阻为R的金属线圈放入磁场中,穿过线圈的磁通量随时间的变化如图所示,在0-t0时间内通过线圈上某位置横截面的电荷量为q,则( )
 一电阻为R的金属线圈放入磁场中,穿过线圈的磁通量随时间的变化如图所示,在0-t0时间内通过线圈上某位置横截面的电荷量为q,则( )
一电阻为R的金属线圈放入磁场中,穿过线圈的磁通量随时间的变化如图所示,在0-t0时间内通过线圈上某位置横截面的电荷量为q,则( )| A. | q=$\frac{{Φ}_{0}}{2R}$ | B. | q=$\frac{{Φ}_{0}}{R}$ | C. | q<$\frac{{Φ}_{0}}{R}$ | D. | q>$\frac{{Φ}_{0}}{R}$ |
1. 如图所示,A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R0为定值电阻.当R2的滑片P在中间时,闭合开关S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势为E,内阻为r且恒定不变,那么,下列说法中正确的是( )
如图所示,A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R0为定值电阻.当R2的滑片P在中间时,闭合开关S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势为E,内阻为r且恒定不变,那么,下列说法中正确的是( )
 如图所示,A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R0为定值电阻.当R2的滑片P在中间时,闭合开关S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势为E,内阻为r且恒定不变,那么,下列说法中正确的是( )
如图所示,A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R0为定值电阻.当R2的滑片P在中间时,闭合开关S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势为E,内阻为r且恒定不变,那么,下列说法中正确的是( )| A. | 若将R2的滑动触头P向a端移动,θ将变大 | |
| B. | 若将R2的滑动触头P向b端移动,且用较强的光照射R1时,那么,小球重新达到稳定后θ将变小 | |
| C. | 若滑动触头P向b端移动,且用较弱的光照射R1时,那么,电压表的示数U的变化量的绝对值与电流表的示数I变化量的绝对值的比值将变大 | |
| D. | 若保持滑动触头P不动,且用较强的光照射R1时,那么,电压表的示数U的变化量的绝对值与电流表的示数I变化量的绝对值的比值不变 |




 电子对湮灭是指电子“e-”和正电子“e+”碰撞后湮灭,产生伽马射线的过程,电子对湮灭是正电子发射计算机断层扫描(PET)及正子湮灭能谱学(PAS)的物理基础.如图所示,在平面直角坐标系xOy上,P点在x轴上,且$\overline{OP}$=2L,Q点在负y轴上某处.在第Ⅰ象限内有平行于y轴的匀强电场,在第Ⅱ象限内有一圆形区域,与x、y轴分别相切于A、C两点,$\overline{OA}$=L,在第Ⅳ象限内有一未知的圆形区域(图中未画出),未知圆形区域和圆形区域内有完全相同的匀强磁场,磁场方向垂直于xOy平面向里.一束速度大小为v0的电子束从A点沿y轴正方向射入磁场,经C点射入电场,最后从P点射出电场区域;另一束速度大小为$\sqrt{2}{v_0}$的正电子束从Q点沿与y轴正向成45°角的方向射入第Ⅳ象限,而后进入未知圆形磁场区域,离开磁场时正好到达P点,且恰好与从P点射出的电子束正碰发生湮灭,即相碰时两束粒子速度方向相反.已知正负电子质量均为m、电量均为e,电子的重力不计.求:
电子对湮灭是指电子“e-”和正电子“e+”碰撞后湮灭,产生伽马射线的过程,电子对湮灭是正电子发射计算机断层扫描(PET)及正子湮灭能谱学(PAS)的物理基础.如图所示,在平面直角坐标系xOy上,P点在x轴上,且$\overline{OP}$=2L,Q点在负y轴上某处.在第Ⅰ象限内有平行于y轴的匀强电场,在第Ⅱ象限内有一圆形区域,与x、y轴分别相切于A、C两点,$\overline{OA}$=L,在第Ⅳ象限内有一未知的圆形区域(图中未画出),未知圆形区域和圆形区域内有完全相同的匀强磁场,磁场方向垂直于xOy平面向里.一束速度大小为v0的电子束从A点沿y轴正方向射入磁场,经C点射入电场,最后从P点射出电场区域;另一束速度大小为$\sqrt{2}{v_0}$的正电子束从Q点沿与y轴正向成45°角的方向射入第Ⅳ象限,而后进入未知圆形磁场区域,离开磁场时正好到达P点,且恰好与从P点射出的电子束正碰发生湮灭,即相碰时两束粒子速度方向相反.已知正负电子质量均为m、电量均为e,电子的重力不计.求:
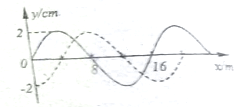 一列简谐横波沿x轴正方向传播,某时刻的波形如图中实线所示,经0.05s后,其波形如图中虚线所示,求:
一列简谐横波沿x轴正方向传播,某时刻的波形如图中实线所示,经0.05s后,其波形如图中虚线所示,求: