题目内容
2.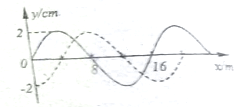 一列简谐横波沿x轴正方向传播,某时刻的波形如图中实线所示,经0.05s后,其波形如图中虚线所示,求:
一列简谐横波沿x轴正方向传播,某时刻的波形如图中实线所示,经0.05s后,其波形如图中虚线所示,求:(1)波长、振幅、8m处质点的振动方向?
(2)若该波的周期大于0.05s,求波速?
(3)若该波的周期小于0.05s,求周期的可能值?
分析 (1)由图读出波长与振幅,并由波的传播方向,来确定质点的振动方向;
(2)据题波的周期大于0.05s,即波传播的时间小于周期,传播的距离不足一个波长,直接读出波传播的距离x,由v=$\frac{v}{t}$ 求解波速.
(3)若该波的周期小于0.05s,根据时间与周期的关系,即可求解.
解答 解:(1)由图知:波长 λ=16m,振幅 A=2cm;
根据波的平移法可知,波沿x轴正方向传播,因此8m处质点的振动方向沿着y轴正方向;
(2)据题:波的周期大于0.05s,即波传播的时间小于周期,传播的距离不足一个波长,又简谐横波沿x轴正方向传播,所以波在0.05s内传播的距离为:x=4m
波速为:v=$\frac{v}{t}$=$\frac{4}{0.05}$m/s=80m/s
(3)由波形的平移法可知:t=0.05s=(n+$\frac{1}{4}$)T,
解得:T=$\frac{1}{20n+5}$s(n=1、2、3…)
答:(1)该波的波长和振幅分别是16m和2cm,而8m处质点的振动方向沿着y轴正方向.
(2)波速是80m/s.
(3)周期的可能值$\frac{1}{20n+5}$s(n=1、2、3…).
点评 本题知道两个时刻的波形,往往要根据空间的周期性或时间的周期性列出波传播距离或周期的通项式,再求特殊值.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
7.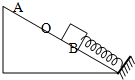 如图所示,一轻弹簧一端与挡板固定,另一端自由伸长时位于O点,当另一端和物块相连时,A、B是物块能保持静止的位置中离挡板最近和最远的点,A、B两点离挡板的距离分别是x1,x2,物块与斜面的最大静摩擦力为f,则弹簧的劲度系数为( )
如图所示,一轻弹簧一端与挡板固定,另一端自由伸长时位于O点,当另一端和物块相连时,A、B是物块能保持静止的位置中离挡板最近和最远的点,A、B两点离挡板的距离分别是x1,x2,物块与斜面的最大静摩擦力为f,则弹簧的劲度系数为( )
 如图所示,一轻弹簧一端与挡板固定,另一端自由伸长时位于O点,当另一端和物块相连时,A、B是物块能保持静止的位置中离挡板最近和最远的点,A、B两点离挡板的距离分别是x1,x2,物块与斜面的最大静摩擦力为f,则弹簧的劲度系数为( )
如图所示,一轻弹簧一端与挡板固定,另一端自由伸长时位于O点,当另一端和物块相连时,A、B是物块能保持静止的位置中离挡板最近和最远的点,A、B两点离挡板的距离分别是x1,x2,物块与斜面的最大静摩擦力为f,则弹簧的劲度系数为( )| A. | $\frac{f}{{x}_{2}+{x}_{1}}$ | B. | $\frac{2f}{{x}_{2}+{x}_{1}}$ | C. | $\frac{2f}{{x}_{2}-{x}_{1}}$ | D. | $\frac{f}{{x}_{2}-{x}_{1}}$ |
11.静止的镭核${\;}_{86}^{226}$Ra发生α(${\;}_{2}^{4}$He)衰变,释放出的α粒子的动能为E,假设衰变时的能量全部以动能形式释放出来,则衰变过程中总的质量亏损是( )
| A. | $\frac{E}{{c}^{2}}$ | B. | $\frac{2E}{111{c}^{2}}$ | C. | $\frac{113E}{111{c}^{2}}$ | D. | $\frac{2E}{{c}^{2}}$ |
 在如图所示的光滑水平面上,小明站在静止的小车上用力向右推静止的木箱,木箱离开手以5m/s的速度向右匀速运动,运动一段时间后与竖直墙壁发生弹性碰撞,反弹回来后被小明接住.已知木箱的质量为30kg,人与车的质量为50kg.求:
在如图所示的光滑水平面上,小明站在静止的小车上用力向右推静止的木箱,木箱离开手以5m/s的速度向右匀速运动,运动一段时间后与竖直墙壁发生弹性碰撞,反弹回来后被小明接住.已知木箱的质量为30kg,人与车的质量为50kg.求: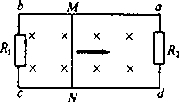 如图所示,在磁感应强度为0.5T的匀强磁场中,让长0.2m的导体棒MN在无摩擦的框架上以5m/s的速度向右匀速运动,电阻R1=R2=2Ω,其他导体的电阻不计.则外力做功的功率有多大?感应电流的功率有多大?在R1和R2上消耗的功率有多大?检验一下:其中的能量转化是否满足守恒定律?
如图所示,在磁感应强度为0.5T的匀强磁场中,让长0.2m的导体棒MN在无摩擦的框架上以5m/s的速度向右匀速运动,电阻R1=R2=2Ω,其他导体的电阻不计.则外力做功的功率有多大?感应电流的功率有多大?在R1和R2上消耗的功率有多大?检验一下:其中的能量转化是否满足守恒定律?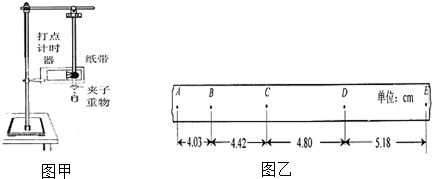
 如图所示,物块A的质量为mA=2.0kg,沿光滑水平面以v0=6$\sqrt{3}$m/s速度水平向右匀速运动,离开平面后刚好落在静止在斜面上的木板B的最上端,且测得物块A所经轨迹到斜面的垂直距离最远.已知斜面足够长,倾角θ=30°,木板B的质量mB=2.0kg,A、B间的动摩擦因数μ1=$\frac{\sqrt{3}}{2}$,B与斜面间的动摩擦因数μ2=$\frac{2\sqrt{3}}{5}$,A在B上运动的过程中恰好没有滑离B木板,所有接触面间的最大摩擦力均等于滑运动摩擦力(g=10m/s2).求:
如图所示,物块A的质量为mA=2.0kg,沿光滑水平面以v0=6$\sqrt{3}$m/s速度水平向右匀速运动,离开平面后刚好落在静止在斜面上的木板B的最上端,且测得物块A所经轨迹到斜面的垂直距离最远.已知斜面足够长,倾角θ=30°,木板B的质量mB=2.0kg,A、B间的动摩擦因数μ1=$\frac{\sqrt{3}}{2}$,B与斜面间的动摩擦因数μ2=$\frac{2\sqrt{3}}{5}$,A在B上运动的过程中恰好没有滑离B木板,所有接触面间的最大摩擦力均等于滑运动摩擦力(g=10m/s2).求: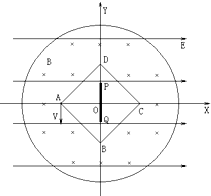 如图所示,在直角坐标系xoy平面内有沿x轴正方向的水平匀强电场,场强为E.在正方形ABCD(O为正方形的中心)与O为圆心半径为2L的圆形之间的区域加垂直纸面向里的匀强磁场,磁感应强度为B.在y轴上有一挡板PQ,挡板长为L,挡板的放置关于x轴对称.A为一个质子源,OA=L,可以向y轴负方向发射出速度从零开始的一系列质子,已知质子的质量为m,电量为q,质子的重力忽略不计.求:
如图所示,在直角坐标系xoy平面内有沿x轴正方向的水平匀强电场,场强为E.在正方形ABCD(O为正方形的中心)与O为圆心半径为2L的圆形之间的区域加垂直纸面向里的匀强磁场,磁感应强度为B.在y轴上有一挡板PQ,挡板长为L,挡板的放置关于x轴对称.A为一个质子源,OA=L,可以向y轴负方向发射出速度从零开始的一系列质子,已知质子的质量为m,电量为q,质子的重力忽略不计.求: