题目内容
18.如图所示,在直角坐标系的xoy第一象限中存在竖直向下的匀强电场,场强大小为4E0,虚线是电场的理想边界线,虚线右端与x轴相交于A(L,0)点,虚线与x轴所围成的空间内没有电场;在第二象限中存在水平向右的匀强电场,场强大小为E0.在M(-L,L)和N(-L,0)两点的连线上有一个粒子发生器装置,可产生质量均为m,电量均为q的静止的带正电的粒子,不计粒子的重力和粒子间的相互作用,且整个装置处于真空中.(1)若粒子从M点由静止开始运动,进入第一象限后始终在电场中运动并恰好到达A点,求该过程中粒子运动时间t及到达A点的速度的大小;
(2)若从MN连线上的各点由静止开始运动的所有粒子,经第一象限的电场偏转穿过虚线后都能到达A点,求此边界线(图中虚线)的方程;
(3)若将第一象限的电场撤去,在第一、四象限中加上垂直平面xoy的圆形区域的匀强磁场,OA为圆形区域的直径,从MN连线上的各点由静止开始运动的一些粒子,经第一象限的磁场偏转后都能从圆形区域的最低点射出磁场,求此匀强磁场的方向和大小.

分析 (1)由牛顿第二定律求得加速度,然后由运动学的公式即可求得运动的时间与到达A的速度;
(2)结合(1)的公式,按照题目的条件写出相应的方程,即可求解;
(3)根据带电粒子在电场中加速,可知,粒子的电性,再根据左手定则,结合粒子在磁场中偏转方向,即可判定磁场的方向,由几何关系,知道已知长度与运动的轨道半径的关系,从而求解磁场的大小.
解答 解:(1)粒子在第二象限从M点由静止开始运动有:
根据牛顿第二定律:E0q=ma1,
匀加速运动位移$L=\frac{1}{2}{a_1}t_1^2$
匀加速运动的末速度${v_1}={a_1}t_1^{\;}$
进入第一象限在电场中类平抛运动有:
根据牛顿第二定律,有4E0q=ma2
竖直方向$y=L=\frac{1}{2}{a_2}t_2^2$
水平方向$x=L={v_1}t_2^{\;}$
竖直分速度${v_y}={a_2}t_2^{\;}$
联立求解得:t=${t_1}+t_2^{\;}=\frac{3}{2}\sqrt{\frac{2mL}{{q{E_0}}}}$
${v_A}=\sqrt{v_y^2+v_1^2}=\sqrt{\frac{{10q{E_0}L}}{m}}$
(2)设从MN连线上的P(-L,y0)点由静止开始运动的某一粒子,经第一象限的电场偏转并通过虚线上的Q(y,x)点后沿直线到达A点,如图
电场E0中加速:${E_0}qL=\frac{1}{2}mv_{{0^{\;}}}^2$
电场4E0中偏转:${y_0}-y=\frac{1}{2}\frac{{4{E_0}q}}{m}t_{\;}^2$
$x=v_{{0^{\;}}}^{\;}t$
${v_y}=\frac{{4{E_0}q}}{m}t$
由图有:$tanθ=\frac{v_y}{v_0}=\frac{y}{L-x}$
联立求得:$y=-\frac{2}{L}x+2{x^2}$且有(0≤x≤L;0≤y≤$\frac{L}{2}$);
(3)粒子在电场E0中加速:${E_0}qL=\frac{1}{2}mv_{{0^{\;}}}^2$
设在磁场中匀速圆周的半径为r,有$r=\frac{{mv_{{0^{\;}}}^{\;}}}{qB}$,由题有$R=\frac{L}{2}$
因PO2、O1Q都在竖直方向,因此四边形PO2QO1为菱形.则r=R
解得 $B=2\sqrt{\frac{{2mE_{{0^{\;}}}^{\;}}}{qL}}$,由左手定则得方向垂直纸面向外
答:(1)该过程中粒子运动时间t为$\frac{3}{2}\sqrt{\frac{2mL}{q{E}_{0}^{\;}}}$及到达A点的速度的大小$\sqrt{\frac{10q{E}_{0}^{\;}L}{m}}$;
(2)此边界线(图中虚线)的方程:$y=-\frac{2}{L}x+2{x^2}$且有(0≤x≤L;0≤y≤$\frac{L}{2}$);
(3)此匀强磁场的方向垂直纸面向外和大小$2\sqrt{\frac{2m{E}_{0}^{\;}}{qL}}$
点评 解答本题的关键是分析粒子的受力情况,再分析运动情况.对于类平抛运动要掌握分解的方法,运用几何知识确定几何关系是关键.

 图中K、L、M为静电场中的3个相距很近的等势线.一带电粒子射入此静电场中后,仅在电场力作用下沿abcde轨迹运动.已知电势φK>φL>φM.下列说法中正确的是( )
图中K、L、M为静电场中的3个相距很近的等势线.一带电粒子射入此静电场中后,仅在电场力作用下沿abcde轨迹运动.已知电势φK>φL>φM.下列说法中正确的是( )| A. | 粒子带负电 | |
| B. | 粒子在bc段做减速运动 | |
| C. | 粒子在a点比e点的速率要大 | |
| D. | 粒子从c点到d点的过程中电场力做负功 |

| A. | 质点振动的周期T=0.2 s | |
| B. | 波速v=20 m/s | |
| C. | 因为一个周期质点运动0.8 m,所以波长λ=0.8 m | |
| D. | 从该时刻起经过0.15 s,波沿x轴正方向传播了3 m | |
| E. | 从该时刻起经过0.25 s时,质点Q的加速度大于质点P的加速度 |
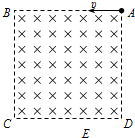 如图所示,边长为L的正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,E点位于CD边上,且ED=$\frac{{\sqrt{3}}}{3}$L,三个完全相同的带电粒子1、2、3分别以大小不同的初速度υ1、υ2、υ3从A点沿AB方向射入该磁场区域,经磁场偏转后粒子1、2、3分别从C点、E点、D点射出.若t1、t2、t3分别表示粒子1、2、3在磁场中的运动时间.则以下判断正确的是( )
如图所示,边长为L的正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,E点位于CD边上,且ED=$\frac{{\sqrt{3}}}{3}$L,三个完全相同的带电粒子1、2、3分别以大小不同的初速度υ1、υ2、υ3从A点沿AB方向射入该磁场区域,经磁场偏转后粒子1、2、3分别从C点、E点、D点射出.若t1、t2、t3分别表示粒子1、2、3在磁场中的运动时间.则以下判断正确的是( )| A. | υ1:υ2:υ3=6:2$\sqrt{3}$:3 | B. | υ1:υ2:υ3=4:3:2 | C. | t1:t2:t3=2:3:4 | D. | t1:t2:t3=3:4:6 |
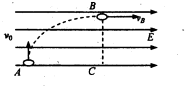 如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )
如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )| A. | $\frac{{mv}_{0}^2}{2q}$ | B. | $\frac{{2mv}_{0}^2}{q}$ | C. | $\frac{{mv}_{0}^2}{q}$ | D. | $\frac{{mv}_{0}^2}{4q}$ |
 如图所示,总质量为460kg的热气球,从地面刚开始竖直上升时的加速度为0.5m/s2,当热气球上升到180m 时,以5m/s的速度向上匀速运动.若离开地面后热气球所受浮力保持不变,上升过程中热气球总质量不变,重力加速度g=10m/s2.关于热气球,下列说法正确的是( )
如图所示,总质量为460kg的热气球,从地面刚开始竖直上升时的加速度为0.5m/s2,当热气球上升到180m 时,以5m/s的速度向上匀速运动.若离开地面后热气球所受浮力保持不变,上升过程中热气球总质量不变,重力加速度g=10m/s2.关于热气球,下列说法正确的是( )| A. | 所受浮力大小为4830 N | |
| B. | 加速上升过程中所受空气阻力保持不变 | |
| C. | 从地面开始上升10 s后的速度大小为5 m/s | |
| D. | 以5 m/s匀速上升时所受空气阻力大小为230 N |
 图为某“全家总动员”节目的情景,高台处的水平轨道AB上装有电动悬挂器,水面上有一半径为R=2m的转盘,其轴心在AB正下方,轴心离高台的水平距离为L=5m,高台边缘与转盘平面的高度差为H=5m.选手抓住悬挂器后,在电动机带动下从平台边缘处由静止开始做加速度为a=2m/s2的匀加速直线运动,在某位置松手后落到转盘上.取g=10m/s2.
图为某“全家总动员”节目的情景,高台处的水平轨道AB上装有电动悬挂器,水面上有一半径为R=2m的转盘,其轴心在AB正下方,轴心离高台的水平距离为L=5m,高台边缘与转盘平面的高度差为H=5m.选手抓住悬挂器后,在电动机带动下从平台边缘处由静止开始做加速度为a=2m/s2的匀加速直线运动,在某位置松手后落到转盘上.取g=10m/s2.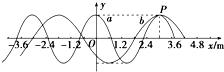 两列简谐横波a、b在同一种均匀介质中沿x轴传播,a波周期为0.5s.某时刻,两列波的波峰正好在xP=3.0m处的P点重合,如图甲所示,则b波的周期为Tb=0.8s,该时刻,离P点最近的波峰重叠点的平衡位置坐标是x=27.0或-21.0m.
两列简谐横波a、b在同一种均匀介质中沿x轴传播,a波周期为0.5s.某时刻,两列波的波峰正好在xP=3.0m处的P点重合,如图甲所示,则b波的周期为Tb=0.8s,该时刻,离P点最近的波峰重叠点的平衡位置坐标是x=27.0或-21.0m.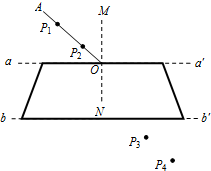 如图所示,在“用插针法测定玻璃的折射率”的实验中,一位同学已完成了部分实验操作,他在白纸上O点画出界面aa′的法线MN,并画出一条带箭头的线段AO作为入射光线.在入射光线上竖直地插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,在P3位置插的大头针正好挡住P1、P2的像,在P4位置插的大头针正好挡住大头针P3和大头针P1、P2的像.根据n=$\frac{sini}{sinr}$可计算出玻璃的折射率,请你在图中完成整个光路图,并标出入射角i和折射角r.
如图所示,在“用插针法测定玻璃的折射率”的实验中,一位同学已完成了部分实验操作,他在白纸上O点画出界面aa′的法线MN,并画出一条带箭头的线段AO作为入射光线.在入射光线上竖直地插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,在P3位置插的大头针正好挡住P1、P2的像,在P4位置插的大头针正好挡住大头针P3和大头针P1、P2的像.根据n=$\frac{sini}{sinr}$可计算出玻璃的折射率,请你在图中完成整个光路图,并标出入射角i和折射角r.