��Ŀ����
3��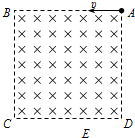 ��ͼ��ʾ���߳�ΪL������������ABCD�ڴ��ڷ���ֱֽ���������ǿ�ų���E��λ��CD���ϣ���ED=$\frac{{\sqrt{3}}}{3}$L��������ȫ��ͬ�Ĵ�������1��2��3�ֱ��Դ�С��ͬ�ij��ٶȦ�1����2����3��A����AB��������ôų������ų�ƫת������1��2��3�ֱ��C�㡢E�㡢D���������t1��t2��t3�ֱ��ʾ����1��2��3�ڴų��е��˶�ʱ�䣮�������ж���ȷ���ǣ�������
��ͼ��ʾ���߳�ΪL������������ABCD�ڴ��ڷ���ֱֽ���������ǿ�ų���E��λ��CD���ϣ���ED=$\frac{{\sqrt{3}}}{3}$L��������ȫ��ͬ�Ĵ�������1��2��3�ֱ��Դ�С��ͬ�ij��ٶȦ�1����2����3��A����AB��������ôų������ų�ƫת������1��2��3�ֱ��C�㡢E�㡢D���������t1��t2��t3�ֱ��ʾ����1��2��3�ڴų��е��˶�ʱ�䣮�������ж���ȷ���ǣ�������| A�� | ��1����2����3=6��2$\sqrt{3}$��3 | B�� | ��1����2����3=4��3��2 | C�� | t1��t2��t3=2��3��4 | D�� | t1��t2��t3=3��4��6 |
���� �����ڴų���������Բ���˶����������ӵ��˶��켣����������ڴų���ת����Բ�Ľǣ�Ȼ��������ӵ��˶�ʱ��֮�ȣ�
��� �⣺�����˶��켣��ͼ��ʾ��
�ɼ���֪ʶ��֪����1=$\frac{��}{2}$����3=�У�
R2cos��+R2=L��R2sin��=ED=$\frac{\sqrt{3}}{3}$L��
��ã�sin��=$\frac{\sqrt{3}}{2}$����=$\frac{��}{3}$����2=��-��$\frac{2��}{3}$��
�����ڴų���������Բ���˶������ڣ�T=$\frac{2��m}{qB}$��ͬ��
�����ڴų��е��˶�ʱ�䣺t=$\frac{��}{2��}$T=$\frac{��m}{qB}$�ئȣ�
�������ڴų��е��˶�ʱ��֮��Ϊ��
t1��t2��t3=��1����2����3=$\frac{��}{2}$��$\frac{2��}{3}$����=3��4��6����ABC����D��ȷ��
��ѡ��D��
���� ���⿼�����������ڴų��е��˶�ʱ��֮�����⣬�����ڴų���������Բ���˶��������������������˶��켣���������ת����Բ�Ľ��ǽ����ǰ����ؼ���Ӧ�����ڹ�ʽ���ɽ��⣮

��ϰ��ϵ�д�
 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
�����Ŀ
14�����ȼ���ֱ���˶����ʵ㣬������A��B��C���㣬��֪AB=BC�����ʵ���AB�ε�ƽ���ٶ�Ϊ6m/s����BC��ƽ���ٶ�Ϊ12m/s��������˵����ȷ���ǣ�������
| A�� | ͨ��AB��BC������ʱ��֮��Ϊ1����$\sqrt{2}$-1�� | |
| B�� | �ʵ���B��ʱ�ٶ�Ϊ9m/s | |
| C�� | �ʵ���B��ʱ�ٶ�Ϊ10m/s | |
| D�� | AB���ʵ��ٶȱ仯����BC���ٶȱ仯��֮��Ϊ2��1 |
11�� һƵ��f=100Hz�IJ�Դ�����ٶ�v=500m/s������ֱ���˶���������ȵ�ʱ�������������ͬʱ������е����ijһʱ�̣������Ļ�е�����˶�ƽ���ϵ������Զλ����ͼ��ʾ����ͼ��ÿ��С������ı߳���ȣ�����û�е���IJ���ԼΪ��������
һƵ��f=100Hz�IJ�Դ�����ٶ�v=500m/s������ֱ���˶���������ȵ�ʱ�������������ͬʱ������е����ijһʱ�̣������Ļ�е�����˶�ƽ���ϵ������Զλ����ͼ��ʾ����ͼ��ÿ��С������ı߳���ȣ�����û�е���IJ���ԼΪ��������
 һƵ��f=100Hz�IJ�Դ�����ٶ�v=500m/s������ֱ���˶���������ȵ�ʱ�������������ͬʱ������е����ijһʱ�̣������Ļ�е�����˶�ƽ���ϵ������Զλ����ͼ��ʾ����ͼ��ÿ��С������ı߳���ȣ�����û�е���IJ���ԼΪ��������
һƵ��f=100Hz�IJ�Դ�����ٶ�v=500m/s������ֱ���˶���������ȵ�ʱ�������������ͬʱ������е����ijһʱ�̣������Ļ�е�����˶�ƽ���ϵ������Զλ����ͼ��ʾ����ͼ��ÿ��С������ı߳���ȣ�����û�е���IJ���ԼΪ��������| A�� | l m | B�� | 3 m | C�� | 5 m | D�� | 7 m |
13�� ��ͼ��ʾ��������������ȣ��ֱ�����硢����Ͳ������С��ƽ�а�糡��˵��е�P����ͬ�ij��ٶ���ˮƽ����ֱ�ڵ糡�������糡�����Ƿֱ�����A��B��C���㣬�����жϣ�������
��ͼ��ʾ��������������ȣ��ֱ�����硢����Ͳ������С��ƽ�а�糡��˵��е�P����ͬ�ij��ٶ���ˮƽ����ֱ�ڵ糡�������糡�����Ƿֱ�����A��B��C���㣬�����жϣ�������
 ��ͼ��ʾ��������������ȣ��ֱ�����硢����Ͳ������С��ƽ�а�糡��˵��е�P����ͬ�ij��ٶ���ˮƽ����ֱ�ڵ糡�������糡�����Ƿֱ�����A��B��C���㣬�����жϣ�������
��ͼ��ʾ��������������ȣ��ֱ�����硢����Ͳ������С��ƽ�а�糡��˵��е�P����ͬ�ij��ٶ���ˮƽ����ֱ�ڵ糡�������糡�����Ƿֱ�����A��B��C���㣬�����жϣ�������| A�� | С��A�����磬B�����磬C������ | |
| B�� | ����С���ڵ糡���˶�ʱ����� | |
| C�� | ����С�K��ʱ�Ķ���EkA��EkB��EkC | |
| D�� | ����С���ڵ糡���˶��ļ��ٶ�aA��aB��aC |
 ��ͼ��ʾ��һ����ƽֱ·����ʻ���������ٶ�Ϊ36km/h��ɲ�����ü��ٶȵĴ�С��4m/s2����
��ͼ��ʾ��һ����ƽֱ·����ʻ���������ٶ�Ϊ36km/h��ɲ�����ü��ٶȵĴ�С��4m/s2����

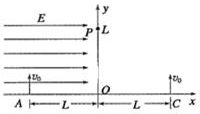 Ϊ�˹۲����������ӵ���ײ���������������õ糡���ų������������������������˶���ʵ����һ���̣�����ͼ��ʾ��xOyƽ���ڣ�A��C��С��ԭ��ľ����ΪL��ÿ��һ����ʱ��ԴԴ���ϵطֱ��A�����������ӣ�C�����븺���ӣ����ٶȾ�Ϊv0���Ҵ�ֱx�ᣬ���������ӵ�������Ϊm���������Ϊe�����Ե���֮�������ã�����y�����������һˮƽ���ҵ���ǿ�糡����y����Ҳ������һ��ֱֽ�����ǿ�ų���ͼ��δ��������Ҫʹ������������y���ϵ�P��0��L������������
Ϊ�˹۲����������ӵ���ײ���������������õ糡���ų������������������������˶���ʵ����һ���̣�����ͼ��ʾ��xOyƽ���ڣ�A��C��С��ԭ��ľ����ΪL��ÿ��һ����ʱ��ԴԴ���ϵطֱ��A�����������ӣ�C�����븺���ӣ����ٶȾ�Ϊv0���Ҵ�ֱx�ᣬ���������ӵ�������Ϊm���������Ϊe�����Ե���֮�������ã�����y�����������һˮƽ���ҵ���ǿ�糡����y����Ҳ������һ��ֱֽ�����ǿ�ų���ͼ��δ��������Ҫʹ������������y���ϵ�P��0��L������������ ��ͼ��ʾ����MN�Ҳ���һ���Ÿ�Ӧǿ��B=0.50T����ǿ�ų����ڴų��е�A����һ��ֹ�غˣ�${\;}_{88}^{236}$Ra����A���MN�ľ���OA=1.0m��DΪ������MN��Ե�����ӽ�������OD=1.0m��${\;}_{88}^{236}$Ra����˥��ʱ���ų�ij����x���Ϊһ뱺ˣ�${\;}_{86}^{222}$Rn����������Dǡ�ý��յ����ش�ֱ��MN��������������x�������Ƽ���ʱ������Ϊ�˵�������������������ԭ������u��1u=1.7��10-27kg��Ԫ���e=1.6��10-19C������ע�������������������λ��Ч���֣�
��ͼ��ʾ����MN�Ҳ���һ���Ÿ�Ӧǿ��B=0.50T����ǿ�ų����ڴų��е�A����һ��ֹ�غˣ�${\;}_{88}^{236}$Ra����A���MN�ľ���OA=1.0m��DΪ������MN��Ե�����ӽ�������OD=1.0m��${\;}_{88}^{236}$Ra����˥��ʱ���ų�ij����x���Ϊһ뱺ˣ�${\;}_{86}^{222}$Rn����������Dǡ�ý��յ����ش�ֱ��MN��������������x�������Ƽ���ʱ������Ϊ�˵�������������������ԭ������u��1u=1.7��10-27kg��Ԫ���e=1.6��10-19C������ע�������������������λ��Ч���֣�