题目内容
12.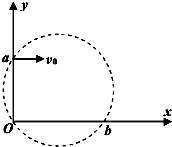 如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)、一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )
如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)、一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )| A. | 电子在磁场中运动的轨道半径为L | |
| B. | 电子在磁场中运动的时间为$\frac{πL}{{v}_{0}}$ | |
| C. | 磁场区域的圆心坐标为($\frac{\sqrt{3}L}{2}$,$\frac{L}{2}$) | |
| D. | 电子在磁场中做圆周运动的圆心坐标为(0,-2L) |
分析 带电粒子在匀强磁场中在洛伦兹力作用下,做匀速圆周运动.所以由几何关系可确定运动圆弧的半径与已知长度的关系,从而确定圆磁场的圆心,并能算出粒子在磁场中运动时间.并根据几何关系来,最终可确定电子在磁场中做圆周运动的圆心坐标.
解答 解:画出粒子运动轨迹如图所示, A、设电子的轨迹半径为R,由几何知识,Rsin30°=R-L,得R=2L,A错误;
A、设电子的轨迹半径为R,由几何知识,Rsin30°=R-L,得R=2L,A错误;
B、电子在磁场中运动时间t=$\frac{60°}{360°}T=\frac{T}{6}$,而 T=$\frac{2πR}{{v}_{0}}$=$\frac{4πL}{{v}_{0}}$,得:t=$\frac{2πL}{3{v}_{0}}$,故B错误;
C、设磁场区域的圆心坐标为(x,y)其中 x=$\frac{1}{2}$Rcos30°=$\frac{\sqrt{3}L}{2}$,y=$\frac{L}{2}$,所以磁场圆心坐标为($\frac{\sqrt{3}L}{2}$,$\frac{L}{2}$),故C正确;
D、根据几何三角函数关系可得,y′=-Rcos60°=-L,所以电子的圆周运动的圆心坐标为(0,-L),故D错误;
故选:C.
点评 由题意确定粒子在磁场中运动轨迹是解题的关键之处,从而求出圆磁场的圆心位置,再运用几何关系来确定电子的运动轨迹的圆心坐标.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
11. 如图所示,传送带AB的倾角为θ,且传送带足够长.现有质量为m可视为质点的物体以v0的初速度从B端开始向上运动,物体与传送带之间的动摩擦因数μ>tanθ,传送带的速度为v(v0<v),方向未知,重力加速度为g.物体在传送带上运动过程中,下列说法正确的是( )
如图所示,传送带AB的倾角为θ,且传送带足够长.现有质量为m可视为质点的物体以v0的初速度从B端开始向上运动,物体与传送带之间的动摩擦因数μ>tanθ,传送带的速度为v(v0<v),方向未知,重力加速度为g.物体在传送带上运动过程中,下列说法正确的是( )
 如图所示,传送带AB的倾角为θ,且传送带足够长.现有质量为m可视为质点的物体以v0的初速度从B端开始向上运动,物体与传送带之间的动摩擦因数μ>tanθ,传送带的速度为v(v0<v),方向未知,重力加速度为g.物体在传送带上运动过程中,下列说法正确的是( )
如图所示,传送带AB的倾角为θ,且传送带足够长.现有质量为m可视为质点的物体以v0的初速度从B端开始向上运动,物体与传送带之间的动摩擦因数μ>tanθ,传送带的速度为v(v0<v),方向未知,重力加速度为g.物体在传送带上运动过程中,下列说法正确的是( )| A. | 摩擦力对物体做功的最大瞬时功率是μmgvcosθ | |
| B. | 摩擦力对物体做功的最大瞬时功率是μmgv0cosθ | |
| C. | 运动过程物体的机械能可能一直增加 | |
| D. | 摩擦力对物体可能先先做正功后做负功 |
12.下列关于摩擦力的说法,正确的是( )
| A. | 相互接触并挤压的两物体间一定存在摩擦力 | |
| B. | 滑动摩擦力总是阻碍物体的运动 | |
| C. | 静止的物体也可以受到滑动摩擦力 | |
| D. | 只有静止的物体才受静摩擦力作用,运动的物体不会受静摩擦力作用 |
17. 某同学家中电视机画面的幅度偏小,维修的技术人员检查后认为是显像管或偏转线圈出了故障,显像管及偏转线圈l如图所示,引起故障的原因可能是( )
某同学家中电视机画面的幅度偏小,维修的技术人员检查后认为是显像管或偏转线圈出了故障,显像管及偏转线圈l如图所示,引起故障的原因可能是( )
 某同学家中电视机画面的幅度偏小,维修的技术人员检查后认为是显像管或偏转线圈出了故障,显像管及偏转线圈l如图所示,引起故障的原因可能是( )
某同学家中电视机画面的幅度偏小,维修的技术人员检查后认为是显像管或偏转线圈出了故障,显像管及偏转线圈l如图所示,引起故障的原因可能是( )| A. | 电子枪发射的电子数减小 | |
| B. | 加速电场的电压过大 | |
| C. | 偏转线圈的电流过小,偏转磁场减弱 | |
| D. | 偏转线圈匝间短路,线圈匝数减小 |
 如图所示,在倾角为37°的斜面上,一个物体以20m/s的速度从A点向上滑行经2s到达最高点B而后折回,求:物体返回时的加速度?(g取10m/s2)
如图所示,在倾角为37°的斜面上,一个物体以20m/s的速度从A点向上滑行经2s到达最高点B而后折回,求:物体返回时的加速度?(g取10m/s2)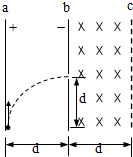 如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,ab间的电场强度为E,今有一带正电的微粒从a板下缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入匀强磁场,磁场区域bc的宽度也为d,磁感应强度方向垂直纸面向里,大小等于$\frac{E}{{v}_{0}}$.求微粒从射入电场到离开磁场所用的时间.
如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,ab间的电场强度为E,今有一带正电的微粒从a板下缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入匀强磁场,磁场区域bc的宽度也为d,磁感应强度方向垂直纸面向里,大小等于$\frac{E}{{v}_{0}}$.求微粒从射入电场到离开磁场所用的时间.
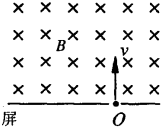 如图所示,匀强磁场的磁感应强度大小为B,方向垂直纸面向里,一个质量为m、电荷量为q的正离子,以速度v从小孔O射入匀强磁场,入射时速度方向既垂直于磁场方向,又与屏垂直,偏转后打在屏上S点(S点未在图上画出),求:
如图所示,匀强磁场的磁感应强度大小为B,方向垂直纸面向里,一个质量为m、电荷量为q的正离子,以速度v从小孔O射入匀强磁场,入射时速度方向既垂直于磁场方向,又与屏垂直,偏转后打在屏上S点(S点未在图上画出),求: 如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻不计.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻.有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T.将一根阻值未知质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好.现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行.(取g=10m/s2,sin 37°=0.6,cos37°=0.8).求:
如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻不计.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻.有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T.将一根阻值未知质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好.现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行.(取g=10m/s2,sin 37°=0.6,cos37°=0.8).求: