题目内容
7.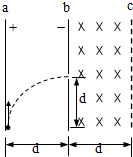 如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,ab间的电场强度为E,今有一带正电的微粒从a板下缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入匀强磁场,磁场区域bc的宽度也为d,磁感应强度方向垂直纸面向里,大小等于$\frac{E}{{v}_{0}}$.求微粒从射入电场到离开磁场所用的时间.
如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,ab间的电场强度为E,今有一带正电的微粒从a板下缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入匀强磁场,磁场区域bc的宽度也为d,磁感应强度方向垂直纸面向里,大小等于$\frac{E}{{v}_{0}}$.求微粒从射入电场到离开磁场所用的时间.
分析 微粒在电场中运动,应用动能定理求出重力与电场力的关系,微粒在竖直方向做匀减速直线运动,应用匀变速直线运动的速度公式求出粒子的运动时间;根据微粒在磁场中的受力情况判断粒子的运动性质,然后求出微粒在磁场中的运动时间,最后求出微粒总的运动时间.
解答 解:从a板到b板,根据动能定理:qEd-mgd=0,
解得:qE=mg,
竖直方向减速运动的时间:${t_1}=\frac{v_0}{g}$;
微粒在磁场中受磁场力:${F_B}=qvB=q{v_0}•\frac{E}{v_0}=qE$,方向向上.
由于:qE=mg,则:FB=mg,微粒在磁场中所受合力为零,
微粒做匀速直线运动,运动时间:${t_2}=\frac{d}{v_0}$,
故总共所用时间为:$t={t_1}+{t_2}=\frac{v_0}{g}+\frac{d}{v_0}$;
答:微粒从射入电场到离开磁场所用的时间为$\frac{{v}_{0}}{g}$+$\frac{d}{{v}_{0}}$.
点评 本题考查了微粒在电磁场中的运动,分析清楚粒子受力情况,判断出粒子运动性质是解题的关键,应用匀变速直线运动与匀速直线运动的运动规律可以解题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
6.关于加速度,以下说法正确的是( )
| A. | 加速度的方向就是速度变化量的方向 | |
| B. | 加速度的大小与△v成正比,与△t成反比 | |
| C. | 加速度的大小正比于速度的大小 | |
| D. | 正的加速度大于负的加速度 |
7. 边长为a的正方形处于有界磁场中,如图所示,一束电子有速度v0水平射入磁场后,分别从A处和C处射出,以下说法正确的是( )
边长为a的正方形处于有界磁场中,如图所示,一束电子有速度v0水平射入磁场后,分别从A处和C处射出,以下说法正确的是( )
 边长为a的正方形处于有界磁场中,如图所示,一束电子有速度v0水平射入磁场后,分别从A处和C处射出,以下说法正确的是( )
边长为a的正方形处于有界磁场中,如图所示,一束电子有速度v0水平射入磁场后,分别从A处和C处射出,以下说法正确的是( )| A. | 从A处和C处射出的电子速度之比为2:1 | |
| B. | 从A处和C处射出的电子在磁场中运动的时间之比为2:1 | |
| C. | 从A处和C处射出的电子在磁场中运动周期之比为2:1 | |
| D. | 从A处和C处射出的电子在磁场中所受洛伦兹力之比为1:2 |
2. 如图所示,在一竖直平面内有水平匀强磁场,磁感应强度为B=2T方向垂直该竖直平面向里,竖直平面中a、b两点在同一水平线上,两点相距l,带电量q=+10×10-19C,质量为m=2.0×10-19kg的质点P,以初速度v从a点对准b点射出,忽略空气阻力,不考虑P与地面接触的可能性,若无论l取什么值,均可使P经直线运动通过b点,若质点的速度取v之外的任意值,可使P必定会经曲线运动通过b点,已知g=10m/s2,则l的值可能为( )
如图所示,在一竖直平面内有水平匀强磁场,磁感应强度为B=2T方向垂直该竖直平面向里,竖直平面中a、b两点在同一水平线上,两点相距l,带电量q=+10×10-19C,质量为m=2.0×10-19kg的质点P,以初速度v从a点对准b点射出,忽略空气阻力,不考虑P与地面接触的可能性,若无论l取什么值,均可使P经直线运动通过b点,若质点的速度取v之外的任意值,可使P必定会经曲线运动通过b点,已知g=10m/s2,则l的值可能为( )
 如图所示,在一竖直平面内有水平匀强磁场,磁感应强度为B=2T方向垂直该竖直平面向里,竖直平面中a、b两点在同一水平线上,两点相距l,带电量q=+10×10-19C,质量为m=2.0×10-19kg的质点P,以初速度v从a点对准b点射出,忽略空气阻力,不考虑P与地面接触的可能性,若无论l取什么值,均可使P经直线运动通过b点,若质点的速度取v之外的任意值,可使P必定会经曲线运动通过b点,已知g=10m/s2,则l的值可能为( )
如图所示,在一竖直平面内有水平匀强磁场,磁感应强度为B=2T方向垂直该竖直平面向里,竖直平面中a、b两点在同一水平线上,两点相距l,带电量q=+10×10-19C,质量为m=2.0×10-19kg的质点P,以初速度v从a点对准b点射出,忽略空气阻力,不考虑P与地面接触的可能性,若无论l取什么值,均可使P经直线运动通过b点,若质点的速度取v之外的任意值,可使P必定会经曲线运动通过b点,已知g=10m/s2,则l的值可能为( )| A. | 50πcm | B. | 60πcm | C. | 70πcm | D. | 80πcm |
12.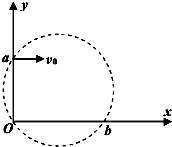 如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)、一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )
如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)、一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )
 如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)、一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )
如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)、一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )| A. | 电子在磁场中运动的轨道半径为L | |
| B. | 电子在磁场中运动的时间为$\frac{πL}{{v}_{0}}$ | |
| C. | 磁场区域的圆心坐标为($\frac{\sqrt{3}L}{2}$,$\frac{L}{2}$) | |
| D. | 电子在磁场中做圆周运动的圆心坐标为(0,-2L) |
16. 法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形铜盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与铜盘接触良好的电刷A、B(A、B间距离为L),两电刷与灵敏电流计相连.当铜盘绕中心轴按图示方向以角速度ω匀速转动时,则下面答案正确的是( )
法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形铜盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与铜盘接触良好的电刷A、B(A、B间距离为L),两电刷与灵敏电流计相连.当铜盘绕中心轴按图示方向以角速度ω匀速转动时,则下面答案正确的是( )
 法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形铜盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与铜盘接触良好的电刷A、B(A、B间距离为L),两电刷与灵敏电流计相连.当铜盘绕中心轴按图示方向以角速度ω匀速转动时,则下面答案正确的是( )
法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形铜盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与铜盘接触良好的电刷A、B(A、B间距离为L),两电刷与灵敏电流计相连.当铜盘绕中心轴按图示方向以角速度ω匀速转动时,则下面答案正确的是( )| A. | 由于穿过铜盘的磁通量不变,故灵敏电流计示数为0 | |
| B. | 盘面可视为无数辐条组成,任何时候都有磁条切割磁感线产生感应电动势 | |
| C. | 电刷A的电势高于电刷B的电势 | |
| D. | A、B间的感应电动势为E=BLω2 |
 如图所示,质量为50kg的人站在与滑轮水平距离为3m处,通过定滑轮将质量为20kg的货物匀速提起,测得滑轮距离地面的高度为5m,人手臂离地面的高度为1m,不!计滑轮大小和摩擦,忽略细绳的重力,人脚与地面间的动摩擦因数为0.5,人的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2.则:
如图所示,质量为50kg的人站在与滑轮水平距离为3m处,通过定滑轮将质量为20kg的货物匀速提起,测得滑轮距离地面的高度为5m,人手臂离地面的高度为1m,不!计滑轮大小和摩擦,忽略细绳的重力,人脚与地面间的动摩擦因数为0.5,人的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2.则: 如图所示,金属棒ab是闭合电路的一部分,水平放置在竖直向下的匀强磁场中,现将金属棒以水平初速度v0向右抛出,设在整个过程中棒始终平动、与棒连接的细导线一直处于松弛状态,不计空气阻力.下列描述下落速度的水平分量大小vx、竖直分量大小vy与时间t的图象,可能正确的是( )
如图所示,金属棒ab是闭合电路的一部分,水平放置在竖直向下的匀强磁场中,现将金属棒以水平初速度v0向右抛出,设在整个过程中棒始终平动、与棒连接的细导线一直处于松弛状态,不计空气阻力.下列描述下落速度的水平分量大小vx、竖直分量大小vy与时间t的图象,可能正确的是( )



 如图所示,纸面内有一直角坐标系xOy,在第一象限内是沿x轴正方向、场强大小为E的匀强电场,在第二象限内是垂直于纸面向里的匀强磁场B(大小未知),在第三、第四象限内是垂直于纸面向外的匀强磁场B′(大小未知),一质量为m,电荷量为e的正粒子从无限靠近y轴的M点以速度v0沿MO方向射出,经x轴上的N点进入第四象限,而后从x轴负半轴N′点(与N点关于O点对称)进入第二象限,最后恰好似沿y轴正方向的速度打在y轴正半轴上,已知tan∠OMN=$\frac{1}{2}$,粒子重力不计,试求:
如图所示,纸面内有一直角坐标系xOy,在第一象限内是沿x轴正方向、场强大小为E的匀强电场,在第二象限内是垂直于纸面向里的匀强磁场B(大小未知),在第三、第四象限内是垂直于纸面向外的匀强磁场B′(大小未知),一质量为m,电荷量为e的正粒子从无限靠近y轴的M点以速度v0沿MO方向射出,经x轴上的N点进入第四象限,而后从x轴负半轴N′点(与N点关于O点对称)进入第二象限,最后恰好似沿y轴正方向的速度打在y轴正半轴上,已知tan∠OMN=$\frac{1}{2}$,粒子重力不计,试求: