题目内容
19.如图所示,两根相距为L的金属轨道固定于水平面上,导轨电阻不计;一根质量为m、长为L、单位长度电阻为R的金属棒两端放于导轨上,导轨与金属棒间的动摩擦因数为μ,棒与导轨的接触电阻不计.导轨左端连有阻值为2R的电阻.轨道平面上有n段竖直向下的宽度为a间距为b的匀强磁场(a>b),磁感应强度为B.金属棒初始位于OO′处,与第一段磁场相距2a.求:
(1)若金属棒有向右的初速度v0,为使金属棒保持v0的速度一直向右穿过各磁场,需对金属棒施加一个水平向右的拉力.求金属棒不在磁场中时受到的拉力F1和在磁场中时受到的拉力F2的大小;
(2)在(1)的情况下,求金属棒从OO′开始运动到刚离开第n段磁场过程中,拉力所做的功;
(3)若金属棒初速度为零,现对其施以水平向右的恒定拉力F,使棒进入各磁场的速度都相同,求金属棒从OO′开始运动到刚离开第n段磁场整个过程中导轨左端电阻上产生的热量.
分析 (1)金属棒在进入磁场前,不受安培力作用,匀速运动时,拉力与摩擦力平衡;在进入磁场后,金属棒切割磁感线,产生感应电流,匀速运动时,拉力与摩擦力和安培力平衡.根据平衡条件和电磁感应知识,可求出拉力.
(2)利用功的公式,求出拉力做的总功.
(3)进入磁场前,拉力和摩擦力做功,根据动能定理,求出金属棒进入磁场时的速度.进入在磁场时,拉力、摩擦力和安培力做功,根据能量守恒定律求出热量
解答 解:(1)金属棒保持v0的速度做匀速运动.
金属棒不在磁场中
F1=f=μmg ①
金属棒在磁场中运动时,电路中的感应电流为I,
F2=f+BIL ②
由闭合电路欧姆定律
I=$\frac{E}{2R+RL}$=$\frac{BL{v}_{0}}{(2+L)R}$ ③
由②③可得
F2=μmg+$\frac{BL{v}_{0}}{(2+L)R}$
(2)金属棒在非磁场区拉力F1所做的功为
W1=F1[2a+(n-1)b]=μmg[2a+(n-1)b]④
金属棒在磁场区拉力F2所做的功为
W2=F2na=(μmg+$\frac{{B}^{2}{L}^{2}{v}_{0}}{(2+L)R}$)na
故拉力做功为:W=W1+W2=μmg[2a+(n-1)b]+nF2a=μmg[2a+(n-1)b]+(μmg+$\frac{{B}^{2}{L}^{2}{v}_{0}}{(2+L)R}$)na
(3)金属棒进入各磁场时的速度均相同,等于从OO’运动2a位移第一次进入磁场时的速度v1,要保证金属棒进入各磁场时的初速度都相同,金属棒在磁场中做减速度运动,离开磁场后再做加速度运动.金属棒每经过一段磁场克服安培力所做的功都相同,设为W电;棒离开每一段磁场时速度也相同,设为v2.由动能定理有
F.a-μmg•a-W电=$\frac{1}{2}$m${v}_{2}^{2}$-$\frac{1}{2}m{v}_{1}^{2}$ ⑦
(F-μmg)b=$\frac{1}{2}m{v}_{1}^{2}$-$\frac{1}{2}m{v}_{2}^{2}$ ⑧
由⑦⑧可得W电=(F-μmg)(a+b)
Q总=nW电
整个过程中导轨左端电阻上产生的热量为
Q=$\frac{2n{W}_{电}}{2+L}$=$\frac{2}{2+L}$n(F-μmg)(a+b)
答:(1)金属棒不在磁场中时受到的拉力F1为μmg,在磁场中时受到的拉力F2的大小为μmg+$\frac{BL{v}_{0}}{(2+L)R}$;
(2)在(1)的情况下,求金属棒从OO′开始运动到刚离开第n段磁场过程中,拉力所做的功为μmg[2a+(n-1)b]+(μmg+$\frac{{B}^{2}{L}^{2}{v}_{0}}{(2+L)R}$)na;
(3)若金属棒初速度为零,现对其施以水平向右的恒定拉力F,使棒进入各磁场的速度都相同,求金属棒从OO′开始运动到刚离开第n段磁场整个过程中导轨左端电阻上产生的热量为$\frac{2n{W}_{电}}{2+L}$=$\frac{2}{2+L}$n(F-μmg)(a+b).
点评 本题分析受力是基础,关键从能量转化和守恒角度来求解,解题时要注意抓住使棒进入各磁场的速度都相同,以及通过每段磁场时电路中发热量均相同的条件.

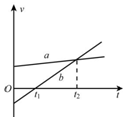 A、B两物体在同一直线上从某点开始计时的速度图象如图中的a、b所示,则由图可知,在0到t2时间内( )
A、B两物体在同一直线上从某点开始计时的速度图象如图中的a、b所示,则由图可知,在0到t2时间内( )| A. | A、B运动始终同向,B比A运动得快 | |
| B. | 在t1时刻,A、B相距最远,B开始反向 | |
| C. | A、B的加速度始终同向,B比A的加速度大 | |
| D. | 在t2时刻,A、B并未相遇,只是速度相同 |
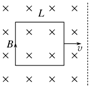 如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )
如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )| A. | 若v1>v2,则拉力F1>F2 | |
| B. | 若v1>v2,则通过导线框截面的电荷量q1>q2 | |
| C. | 若v1>v2,则拉力的功率P1=2P2 | |
| D. | 若v1>v2,则线框中产生的热量Q1=2Q2 |
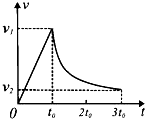 在“跨越-2015•朱日和”系列军事演习中,某部伞兵进行了飞行跳伞演习,该伞兵从高空静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地,他的速度随时间变化的规律如图所示,其中0~t0内是直线,下列结论正确的是( )
在“跨越-2015•朱日和”系列军事演习中,某部伞兵进行了飞行跳伞演习,该伞兵从高空静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地,他的速度随时间变化的规律如图所示,其中0~t0内是直线,下列结论正确的是( )| A. | 伞兵在0~t0时间内加速度不变,在t0~3t0时间内加速度增大 | |
| B. | 伞兵在t0~3t0时间内,平均速度为$\frac{{v}_{1}+{v}_{2}}{2}$ | |
| C. | 降落伞打开后,降落伞和伞兵所受的阻力越来越小 | |
| D. | 降落伞打开后,降落伞和伞兵所受的阻力大小恒定 |
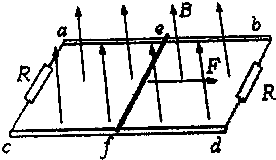 如图所示,两根间距L=1.0m、足够长平行光滑金属导轨ab、cd水平放置,两端均与阻值R=2.0Ω的电阻相连.质量m=0.2kg的导体棒ef在恒定外力F作用下由静止开始运动,导体棒长度与两导轨间距相等,导体棒电阻为r=1.0Ω,整个装置处于垂直于导轨平面向上的匀强磁场B中,导体棒运动过程中与金属导轨接触良好(两导轨及导线电阻不计).求:
如图所示,两根间距L=1.0m、足够长平行光滑金属导轨ab、cd水平放置,两端均与阻值R=2.0Ω的电阻相连.质量m=0.2kg的导体棒ef在恒定外力F作用下由静止开始运动,导体棒长度与两导轨间距相等,导体棒电阻为r=1.0Ω,整个装置处于垂直于导轨平面向上的匀强磁场B中,导体棒运动过程中与金属导轨接触良好(两导轨及导线电阻不计).求: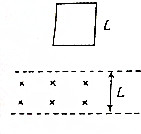 如图所示,间距为L的两水平虚线间存在垂直纸面向里的水平匀强磁场,一边长为L的正方形闭合金属线框自上方某处自由释放,线框平面始终在同一竖直平面内,下边始终水平,以刚进入磁场时为计时起点,则线框所受安培力F大小随时间t变化的关系图线可能为( )
如图所示,间距为L的两水平虚线间存在垂直纸面向里的水平匀强磁场,一边长为L的正方形闭合金属线框自上方某处自由释放,线框平面始终在同一竖直平面内,下边始终水平,以刚进入磁场时为计时起点,则线框所受安培力F大小随时间t变化的关系图线可能为( )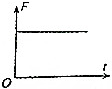


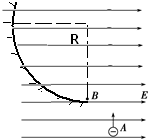 如图所示,在水平向右的匀强电场中的A点,有一个质量为m、带电荷量为-q的小球以速度v竖直向上运动.已知当小球经过最高点B时(AB的竖直距离为h),速度恰变成水平方向,大小也为v.并恰好进入B点的左侧半径为R(R足够大)的光滑圆弧形轨道,求:
如图所示,在水平向右的匀强电场中的A点,有一个质量为m、带电荷量为-q的小球以速度v竖直向上运动.已知当小球经过最高点B时(AB的竖直距离为h),速度恰变成水平方向,大小也为v.并恰好进入B点的左侧半径为R(R足够大)的光滑圆弧形轨道,求: 如图所示,在竖直放置的足够大的铅屏A的右表面上贴着β 射线(即电子)放射源P,已知射线实质为高速电子流,放射源放出β 粒子的速度为v0.足够大的荧光屏M与铅屏A平行放置,相距为d,其间有水平向左的匀强电场,电场强度大小为E.已知电子电量为e,电子质量为m.求:
如图所示,在竖直放置的足够大的铅屏A的右表面上贴着β 射线(即电子)放射源P,已知射线实质为高速电子流,放射源放出β 粒子的速度为v0.足够大的荧光屏M与铅屏A平行放置,相距为d,其间有水平向左的匀强电场,电场强度大小为E.已知电子电量为e,电子质量为m.求: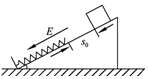 如图所示,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g.
如图所示,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g.