题目内容
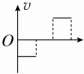
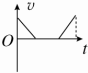
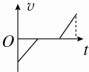
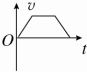
7．
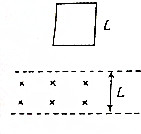如图所示，间距为L的两水平虚线间存在垂直纸面向里的水平匀强磁场，一边长为L的正方形闭合金属线框自上方某处自由释放，线框平面始终在同一竖直平面内，下边始终水平，以刚进入磁场时为计时起点，则线框所受安培力F大小随时间t变化的关系图线可能为（ ）| A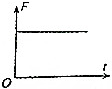． |  | B． |  | C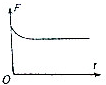． |  | D． |  |
分析 根据安培力表达式F=BIL，及I=$\frac{E}{R}$，E=BLv，从而确定安培力F与线框的速度关系，再分析线框所受安培力FA随时间t变化的情况．
解答 解：线框在进入磁场的过程中，产生的感应电动势E=BLv，而感应电流I=$\frac{E}{R}$=$\frac{BLv}{R}$，
那么线框受到的安培力F=BIL=$\frac{{B}^{2}{L}^{2}v}{R}$；
当线框进入磁场时，安培力等于重力，匀速运动，则安培力大小不随时间变化，
当线框进入磁场时，安培力大于重力，先减速运动，当安培力等于重力时，则做匀速运动直线，那么安培力大小随时间先减小，后不变，
当线框进入磁场时，安培力小于重力，先加速运动，当安培力等于重力时，则做匀速运动直线，那么安培力大小随时间先增大，后不变，故ABC正确，D错误．
故选：ABC．
点评 本题先分析线框进入磁场的运动情况，再判断线框出磁场时安培力与重力关系，判断其运动情况，考查分析和判断线框受力情况和运动情况的能力．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，处于匀强磁场中的两根足够长，电阻不计的光滑平面金属导轨相距1m，导轨平面与水平面成θ=37°角，下端连接阻值R=2Ω的电阻匀强磁场方向垂直导轨平面向上，磁感应强度B=1T．质量m=0.2kg，电阻不计的金属棒放在两导轨上，棒与导轨垂直并保持良好接触．（sin37°=0.6，cos37°=0.8，g=10m/s2），试求
15．
如图所示，带正电荷量为q、质量为m的滑块，沿固定绝缘斜面匀速下滑，现加一竖直向上的匀强电场，电场强度为E，且qE≤mg，以下判断中，正确的是（ ）
如图所示，带正电荷量为q、质量为m的滑块，沿固定绝缘斜面匀速下滑，现加一竖直向上的匀强电场，电场强度为E，且qE≤mg，以下判断中，正确的是（ ）| A． | 物体将保持匀速下滑 | B． | 物体将沿斜面加速下滑 | ||
| C． | 物体将沿斜面减速下滑 | D． | 不能确定物体的运动状态 |
如图1所示，不计电阻的平行金属导轨竖直放置，导轨间距为L，上端接有电阻R，虚线MN下方是垂直于导轨平面的磁场（图中未画出），同一水平高度各处磁感应强度相同，从虚线MN开始建立竖直向下的坐标轴y（坐标原点O在虚线MN上），磁感应强度B与y关系为：B=B0sin（$\frac{π}{d}y$），如图2所示，图中B0、d为已知量，现将质量为m、电阻为r的金属杆ab，从距MN高h处垂直导轨由静止释放，杆下落过程中始终与导轨保持良好接触，重力加速度为g，求：
12．
如图甲所示，光滑的平行竖直金属导轨AB、CD相距L，在A、C之间接一个阻值为R的电阻，在两导轨间abcd矩形区域内有垂直导轨平面向外、长为5d的匀强磁场，磁感应强度为B，一质量为m、电阻为r、长度也刚好为L的导体棒放在磁场下边界ab上（与ab边重合），现用一个竖直向上的力F拉导体棒，使它由静止开始运动，导体棒刚要离开磁场时做匀速直线运动，导体棒与导轨始终垂直且保持良好接触，导轨电阻不计，F随导体棒与初始位置的距离x变化的情况如图乙所示，已知重力加速度为g，下列判断正确的是（ ）
如图甲所示，光滑的平行竖直金属导轨AB、CD相距L，在A、C之间接一个阻值为R的电阻，在两导轨间abcd矩形区域内有垂直导轨平面向外、长为5d的匀强磁场，磁感应强度为B，一质量为m、电阻为r、长度也刚好为L的导体棒放在磁场下边界ab上（与ab边重合），现用一个竖直向上的力F拉导体棒，使它由静止开始运动，导体棒刚要离开磁场时做匀速直线运动，导体棒与导轨始终垂直且保持良好接触，导轨电阻不计，F随导体棒与初始位置的距离x变化的情况如图乙所示，已知重力加速度为g，下列判断正确的是（ ）| A． | 导体棒离开磁场时速度大小为$\frac{2mg（R+r）}{{B}^{2}{L}^{2}}$ | |
| B． | 导体棒经过磁场的过程中，通过电阻R的电荷量为$\frac{5BLd}{R}$ | |
| C． | 离开磁场时导体棒两端电压为$\frac{2mgR}{BL}$ | |
| D． | 导体棒经过磁场的过程中，电阻R产生焦耳热为$\frac{9mgdR{B}^{4}{L}^{4}-2{m}^{3}{g}^{2}R（R+r）^{2}}{{B}^{4}{L}^{4}（R+r）}$ |
如图所示，一电荷量q=+3×10-5C的小球，用绝缘细线悬挂于竖直放置足够大的平行金属板中的O点．电键S合上后，小球静止时细线与竖直方向的夹角θ=37°．已知两板间距d=0.1m，电源电动势E=15V，内阻r=0.5Ω，电阻R1=3Ω，R2=R3=R4=8Ω，．取g=10m/s2，已知sin37°=0.6，cos37°=0.8．求：
2016年8月24日中国青年网消息，北京被称作“最能装”的8A型列车正式亮相，最大载客量达到3456人．该列车匀减速进站，停靠一段时间后又匀加速（同方向）出站，在如图所示的四个v-t图象中，正确描述了火车运动情况的是（ ）
