��Ŀ����
10��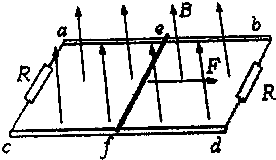 ��ͼ��ʾ���������L=1.0m���㹻��ƽ�й⻬��������ab��cdˮƽ���ã����˾�����ֵR=2.0���ĵ�������������m=0.2kg�ĵ����ef�ں㶨����F�������ɾ�ֹ��ʼ�˶������������������������ȣ����������Ϊr=1.0��������װ�ô��ڴ�ֱ�ڵ���ƽ�����ϵ���ǿ�ų�B�У�������˶����������������Ӵ����ã������켰���ߵ��費�ƣ�����
��ͼ��ʾ���������L=1.0m���㹻��ƽ�й⻬��������ab��cdˮƽ���ã����˾�����ֵR=2.0���ĵ�������������m=0.2kg�ĵ����ef�ں㶨����F�������ɾ�ֹ��ʼ�˶������������������������ȣ����������Ϊr=1.0��������װ�ô��ڴ�ֱ�ڵ���ƽ�����ϵ���ǿ�ų�B�У�������˶����������������Ӵ����ã������켰���ߵ��費�ƣ�������1����������ٶ�Ϊvʱ�������ܰ�����F����С�ı���ʽ������������ĸ��ʾ��
��2��ef���ܴﵽ������ٶ�vm�ı���ʽ������������ĸ��ʾ��
��3������֪�㶨����F=1N���Ÿ�Ӧǿ��B=1T��ef���ܴﵽ������ٶ�vm=2m/s����ef���ɾ�ֹ��ʼ�˶�����Ϊs=5.4mʱ���ٶ��Ѿ��ﵽ2m/s������˹�����������·�����Ľ�����Q��
���� ��1����������ٶ�Ϊvʱ�����ݷ����ڵ�Ÿ�Ӧ��������Ӧ�綯�ƣ����ݱպϵ�·��ŷķ�������ͨ��������ĵ���ǿ�ȣ����ݰ������ļ��㹫ʽ�������ܰ�����F����С�ı���ʽ��
��2������������������ʱ���ٶ�����ɴ�������ʽ��
��3�������˶�ʱ�������ڰ����������������С���ٸ��ݶ��ܶ����������Ľ����ȣ�
��� �⣺��1����������ٶ�Ϊvʱ�������ĸ�Ӧ�綯��Ϊ��E=BLv��
ͨ��������ĵ���ǿ��Ϊ��$I=\frac{BLv}{r+\frac{R}{2}}=\frac{2BLv}{2r+R}$
�����ܰ�����F����С�ı���ʽΪ��F��=BIL=$\frac{2{B}^{2}{L}^{2}v}{2r+R}$��
��2������������������ʱ���ٶ�������У�F=$\frac{2{B}^{2}{L}^{2}{v}_{m}}{2r+R}$��
��ã�${v}_{m}=\frac{F��2r+R��}{2{B}^{2}{L}^{2}}$��
��3�������˶�ʱ�������ڰ��������У�F=$\frac{2{B}^{2}{L}^{2}{v}_{m}}{2r+R}$=$\frac{2��{1}^{2}��{1}^{2}��2}{2��1+2}N=1N$��
���ݶ��ܶ����ɵã�Fs-Q=$\frac{1}{2}m{v}_{m}^{2}$-0��
��ã�Q=5.0J��
�𣺣�1����������ٶ�Ϊvʱ�������ܰ�����F��=$\frac{2{B}^{2}{L}^{2}v}{2r+R}$��
��2��ef���ܴﵽ������ٶ�vm�ı���ʽ${v}_{m}=\frac{F��2r+R��}{2{B}^{2}{L}^{2}}$��
��3���˹�����������·�����Ľ�����Ϊ5.0J��
���� ���ڵ�Ÿ�Ӧ�����о�˼·������������һ�������ĽǶȣ��ص��Ƿ��������������������ƽ�����⣻��һ����������������Ÿ�Ӧ�����е��������ת���ǹؼ���

 ��ͼ��ƽ�а������������������ˮƽ�����һ�ǶȦȣ���������һֱ����Դ��������һ����Ϊm�Ĵ�������ǡ����ͼ����ʾˮƽֱ��ͨ�������������ڴ˹����У������ӣ�������
��ͼ��ƽ�а������������������ˮƽ�����һ�ǶȦȣ���������һֱ����Դ��������һ����Ϊm�Ĵ�������ǡ����ͼ����ʾˮƽֱ��ͨ�������������ڴ˹����У������ӣ�������| A�� | һ�������� | B�� | �ܵ��ĵ糡��F=mgtan�� | ||
| C�� | ��������С | D�� | ���ܼ�С |
 ��ͼ��ʾ�����������Ϊq������Ϊm�Ļ��飬�ع̶���Եб�������»����ּ�һ��ֱ���ϵ���ǿ�糡���糡ǿ��ΪE����qE��mg�������ж��У���ȷ���ǣ�������
��ͼ��ʾ�����������Ϊq������Ϊm�Ļ��飬�ع̶���Եб�������»����ּ�һ��ֱ���ϵ���ǿ�糡���糡ǿ��ΪE����qE��mg�������ж��У���ȷ���ǣ�������| A�� | ���彫���������»� | B�� | ���彫��б������»� | ||
| C�� | ���彫��б������»� | D�� | ����ȷ��������˶�״̬ |
| A�� | ��ѹ���ֲ��䣬�������� | B�� | ��ѹ���ֲ��䣬����������� | ||
| C�� | ��ѹ���ֲ��䣬��С�����ľ��� | D�� | ���ϴ�ʩ������ |
 ��ͼ��ʾ��ˮƽ�������ǿ�糡�У��ó�Ϊl�ľ�Ե����ϸ������һС��С������Ϊm��������Ϊ+q����С��������ֱλ�����λ��A�㴦�����ͷţ�С������ڶ���ϸ������ƫ����ֱ��������ǶȦ�=74�㣮[$\frac{��1-cos�ȣ�}{sin��}$=tan��$\frac{��}{2}$��]
��ͼ��ʾ��ˮƽ�������ǿ�糡�У��ó�Ϊl�ľ�Ե����ϸ������һС��С������Ϊm��������Ϊ+q����С��������ֱλ�����λ��A�㴦�����ͷţ�С������ڶ���ϸ������ƫ����ֱ��������ǶȦ�=74�㣮[$\frac{��1-cos�ȣ�}{sin��}$=tan��$\frac{��}{2}$��] ��ͼ��ʾ��������ǿ�ų��е������㹻�������費�ƵĹ⻬ƽ������������1m������ƽ����ˮƽ��ɦ�=37��ǣ��¶�������ֵR=2���ĵ�����ǿ�ų�����ֱ����ƽ�����ϣ��Ÿ�Ӧǿ��B=1T������m=0.2kg�����費�ƵĽ����������������ϣ����뵼�촹ֱ���������ýӴ�����sin37��=0.6��cos37��=0.8��g=10m/s2��������
��ͼ��ʾ��������ǿ�ų��е������㹻�������費�ƵĹ⻬ƽ������������1m������ƽ����ˮƽ��ɦ�=37��ǣ��¶�������ֵR=2���ĵ�����ǿ�ų�����ֱ����ƽ�����ϣ��Ÿ�Ӧǿ��B=1T������m=0.2kg�����費�ƵĽ����������������ϣ����뵼�촹ֱ���������ýӴ�����sin37��=0.6��cos37��=0.8��g=10m/s2�������� ��ͼ1��ʾ�����Ƶ����ƽ�н���������ֱ���ã�������ΪL���϶˽��е���R������MN�·��Ǵ�ֱ�ڵ���ƽ��Ĵų���ͼ��δ��������ͬһˮƽ�߶ȸ����Ÿ�Ӧǿ����ͬ��������MN��ʼ������ֱ���µ�������y������ԭ��O������MN�ϣ����Ÿ�Ӧǿ��B��y��ϵΪ��B=B0sin��$\frac{��}{d}y$������ͼ2��ʾ��ͼ��B0��dΪ��֪�����ֽ�����Ϊm������Ϊr�Ľ�����ab���Ӿ�MN��h����ֱ�����ɾ�ֹ�ͷţ������������ʼ���뵼�챣�����ýӴ����������ٶ�Ϊg����
��ͼ1��ʾ�����Ƶ����ƽ�н���������ֱ���ã�������ΪL���϶˽��е���R������MN�·��Ǵ�ֱ�ڵ���ƽ��Ĵų���ͼ��δ��������ͬһˮƽ�߶ȸ����Ÿ�Ӧǿ����ͬ��������MN��ʼ������ֱ���µ�������y������ԭ��O������MN�ϣ����Ÿ�Ӧǿ��B��y��ϵΪ��B=B0sin��$\frac{��}{d}y$������ͼ2��ʾ��ͼ��B0��dΪ��֪�����ֽ�����Ϊm������Ϊr�Ľ�����ab���Ӿ�MN��h����ֱ�����ɾ�ֹ�ͷţ������������ʼ���뵼�챣�����ýӴ����������ٶ�Ϊg����