题目内容
6.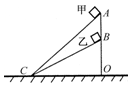 如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )
如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )| A. | Ek1>Ek2 | B. | v1>v2 | ||
| C. | W1<W2 | D. | t1与t2大小关系不确定 |
分析 通过动能定理得到动能的关系式,进而判断两动能大小;由动能得到速度关系式,克服摩擦力做功直接按功的定义式求解,运动时间由匀变速直线运动规律求解.
解答 解:A、设斜面与水平面的夹角为θ,OC=L,那么,物体从斜面顶点滑到底端过程只有重力、摩擦力做功,故有动能定理可得:${E}_{k}=mgLtanθ-μmgcosθ•\frac{L}{cosθ}=mgL(tanθ-μ)$,故Ek和θ,m成正相关,又有θ1>θ2,m1<m2,故Ek1、Ek2,不能比较大小,故A错误;
B、${E}_{k}=\frac{1}{2}m{v}^{2}$,故由A可得:$v=\sqrt{2gL(tanθ-μ)}$,故θ越大,v越大,所以,v1>v2,故B正确;
C、甲、乙在下滑至底端C的过程中克服摩擦力做的功$W=μmgcosθ•\frac{L}{cosθ}=μmgL$,故m越大,W越大,所以,W1<W2,故C正确;
D、物体受力不变,故沿斜面向下做匀加速直线运动,由牛顿第二定律可得:加速度a=gsinθ-μgcosθ,那么物体下滑位移为$\frac{L}{cosθ}$,运动时间$t=\sqrt{\frac{2\frac{L}{cosθ}}{gsinθ-μgcosθ}}=\sqrt{\frac{2L}{g}•\frac{1}{cosθ(sinθ-μcosθ)}}$,故t和θ的竖直相关,但无同步变化规律,θ增大,t可能增大也可能减小,故t1与t2大小关系不确定,故D正确;
故选:BCD.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
6.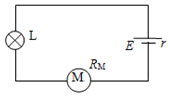 如图所示,电源内阻不可忽略,电路中接有一小灯泡和一电动机.小灯泡L上标有“9V 9W”字样,电动机的线圈电阻RM=1Ω.若灯泡正常发光时,电源的输出电压为15V,此时( )
如图所示,电源内阻不可忽略,电路中接有一小灯泡和一电动机.小灯泡L上标有“9V 9W”字样,电动机的线圈电阻RM=1Ω.若灯泡正常发光时,电源的输出电压为15V,此时( )
 如图所示,电源内阻不可忽略,电路中接有一小灯泡和一电动机.小灯泡L上标有“9V 9W”字样,电动机的线圈电阻RM=1Ω.若灯泡正常发光时,电源的输出电压为15V,此时( )
如图所示,电源内阻不可忽略,电路中接有一小灯泡和一电动机.小灯泡L上标有“9V 9W”字样,电动机的线圈电阻RM=1Ω.若灯泡正常发光时,电源的输出电压为15V,此时( )| A. | 整个电路消耗的电功率为15 W | B. | 电动机的输出功率为5 W | ||
| C. | 电动机的热功率为6 W | D. | 电动机的输入功率为6 W |
7.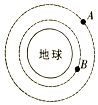 如图所示,两质量相等的卫星A、B绕地球做匀速圆周运动,用R、T、Ek、S分别表示卫星的轨道半径、周期、动能、与地心连线在单位时间内扫过的面积.下列关系式正确的是( )
如图所示,两质量相等的卫星A、B绕地球做匀速圆周运动,用R、T、Ek、S分别表示卫星的轨道半径、周期、动能、与地心连线在单位时间内扫过的面积.下列关系式正确的是( )
 如图所示,两质量相等的卫星A、B绕地球做匀速圆周运动,用R、T、Ek、S分别表示卫星的轨道半径、周期、动能、与地心连线在单位时间内扫过的面积.下列关系式正确的是( )
如图所示,两质量相等的卫星A、B绕地球做匀速圆周运动,用R、T、Ek、S分别表示卫星的轨道半径、周期、动能、与地心连线在单位时间内扫过的面积.下列关系式正确的是( )| A. | TA<TB | B. | EkA>EkB | ||
| C. | SA=SB | D. | $\frac{{R}_{A}^{3}}{{T}_{A}^{2}}$=$\frac{{R}_{B}^{3}}{{T}_{B}^{2}}$ |
1.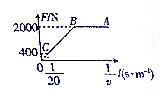 在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )
在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )
 在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )
在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )| A. | 在AB过程中,电动车做匀加速运动 | |
| B. | 在整个过程中,电动车受到的阻力为2000N | |
| C. | 在整个过程中,电动车发动机的最大功率为8000W | |
| D. | 在整个过程中,电动车克服阻力做的功为72000J |
18.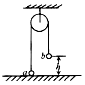 如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
 如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )| A. | $\frac{m}{M+m}$h | B. | $\frac{M}{M+m}$h | C. | $\frac{2m}{M+m}$h | D. | $\frac{2M}{M+m}$h |
16.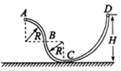 由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )
由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )
 由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )
由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )| A. | 若小球恰好能够到达水平管口A处,则H>2R | |
| B. | 若小球恰好能够到达水平管口A处,则H=2R | |
| C. | 若小球通过A处时对管壁恰好无压力,则H=$\frac{1}{2}$R | |
| D. | 若小球通过A处时对管壁恰好无压力,则H=$\frac{5}{2}$R |
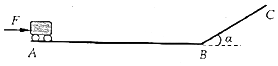 如图所示,长为L的水平面AB与倾角α=30°的斜面BC在B点平滑连接,水平面上质量为m的小推车从A处由静止开始,在沿水平方向的恒定推力F作用下运动.当小推车通过B点后撤去推力,靠惯性滑行到达斜面顶端时速度刚好减为零.已知小推车与水平面和斜面间的动摩擦因数均为μ,重力加速度大小为g,求:
如图所示,长为L的水平面AB与倾角α=30°的斜面BC在B点平滑连接,水平面上质量为m的小推车从A处由静止开始,在沿水平方向的恒定推力F作用下运动.当小推车通过B点后撤去推力,靠惯性滑行到达斜面顶端时速度刚好减为零.已知小推车与水平面和斜面间的动摩擦因数均为μ,重力加速度大小为g,求: