题目内容
15.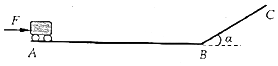 如图所示,长为L的水平面AB与倾角α=30°的斜面BC在B点平滑连接,水平面上质量为m的小推车从A处由静止开始,在沿水平方向的恒定推力F作用下运动.当小推车通过B点后撤去推力,靠惯性滑行到达斜面顶端时速度刚好减为零.已知小推车与水平面和斜面间的动摩擦因数均为μ,重力加速度大小为g,求:
如图所示,长为L的水平面AB与倾角α=30°的斜面BC在B点平滑连接,水平面上质量为m的小推车从A处由静止开始,在沿水平方向的恒定推力F作用下运动.当小推车通过B点后撤去推力,靠惯性滑行到达斜面顶端时速度刚好减为零.已知小推车与水平面和斜面间的动摩擦因数均为μ,重力加速度大小为g,求:(1)小推车到达B点时推力的功率;
(2)小推车在斜面上由B运动到C的过程中克服摩擦力做的功.
分析 (1)根据动能定理求得推车在B的速度,然后由瞬时功率的定义式求得功率;
(2)根据功的定义式求得BC运动过程中重力、摩擦力做的功,然后对该过程应用动能定理即可联立求解.
解答 解:(1)小推车由A运动到B过程中只有推力、摩擦力做功,故由动能定理可得:$FL-μmgL=\frac{1}{2}m{{v}_{B}}^{2}$
解得:${v}_{B}=\sqrt{\frac{2(F-μmg)L}{m}}$;
所以,小推车到达B点时推力的功率为:$P=F{v}_{B}=F\sqrt{\frac{2(F-μmg)L}{m}}$;
(2)小推车在BC上运动只有摩擦力、重力做功,且f=μmgcosθ,从B到C克服摩擦力做功为:-Wf=μmgBCcosθ=$\frac{\sqrt{3}}{2}μmgBC$
重力做功为:${W}_{G}=-mgBCsinθ=-\frac{1}{2}mgBC$;
小推车从B到C只有重力、摩擦力做功,故由动能定理可得:${W}_{f}+{W}_{G}=-mgBC(\frac{\sqrt{3}}{2}μ+\frac{1}{2})=0-\frac{1}{2}m{{v}_{B}}^{2}=-FL+μmgL$
所以,小推车在斜面上由B运动到C的过程中克服摩擦力做的功为:$-{W}_{f}=\frac{\sqrt{3}}{2}μmgBC=\frac{\sqrt{3}}{2}μ\frac{FL-μmgL}{\frac{\sqrt{3}}{2}μ+\frac{1}{2}}$=$\frac{\sqrt{3}μL(F-μmg)}{\sqrt{3}μ+1}$;
答:(1)小推车到达B点时推力的功率为$F\sqrt{\frac{2(F-μmg)L}{m}}$;
(2)小推车在斜面上由B运动到C的过程中克服摩擦力做的功为$\frac{\sqrt{3}μL(F-μmg)}{\sqrt{3}μ+1}$.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

| A. | 将同一单摆从山下移到山上,其振动频率减小 | |
| B. | 单摆摆球的回复力是摆球重力沿圆弧切线方向的分力 | |
| C. | 用一装满砂的轻漏斗做成单摆,在开始振动后砂从漏斗中慢慢漏出的过程中,其振动周期逐渐变大 | |
| D. | 单摆在正向最大位移处时的位移为-A(A为振幅) |
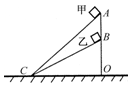 如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )
如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )| A. | Ek1>Ek2 | B. | v1>v2 | ||
| C. | W1<W2 | D. | t1与t2大小关系不确定 |
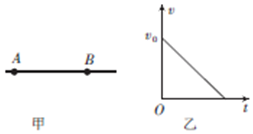 如图甲所示,A、B是一条电场线上的两点,一质子只在电场力作用下,以初速度v0由A点运动到B点,其速度-时间如图乙所示,质子到达B点时速度恰为零,下列判断正确的是( )
如图甲所示,A、B是一条电场线上的两点,一质子只在电场力作用下,以初速度v0由A点运动到B点,其速度-时间如图乙所示,质子到达B点时速度恰为零,下列判断正确的是( )| A. | 该电场可能是由正点电荷产生的 | |
| B. | A点的电场强度与B点的相同 | |
| C. | A点的电势低于B点的电势 | |
| D. | 质子在AB中点时的速度大小为$\frac{{\sqrt{2}}}{2}{v_0}$ |
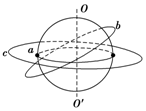 如图所示,a为赤道上的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球的同步卫星,已知地球半径为R,地球同步卫星轨道半径为6.6R;下列说法中正确的是( )
如图所示,a为赤道上的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球的同步卫星,已知地球半径为R,地球同步卫星轨道半径为6.6R;下列说法中正确的是( )| A. | a和c的向心加速度之比为1:6.6 | B. | b和c的向心加速度之比为6.6:1 | ||
| C. | a的运转周期大于c的运转周期 | D. | b的运转周期大于c的运转周期 |
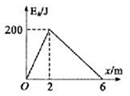 物体在水平桌面上受到水平恒定拉力作用由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )
物体在水平桌面上受到水平恒定拉力作用由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )| A. | 物块的质量 | B. | 物块与桌面之间的滑动摩擦力 | ||
| C. | 水平拉力大小 | D. | 物块在前0~2m内的加速度 |
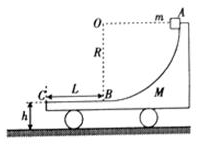 如图所示,质量M=2kg的小车静止在光滑的水平面上,小车AB部分是半径R=0.3m的四分之一光滑圆弧轨道,BC部分是长L=0.25m的水平粗糙轨道,两段轨道相切于B点,水平轨道左端C离地面高度h=0.1m.质量m=lkg的小物块(视为质点)在小车上A点从静止沿轨道下滑,物块与水平轨道间的动摩擦因数μ=0.6,重力加速度取g=10m/s2,求:
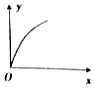
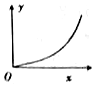
如图所示,质量M=2kg的小车静止在光滑的水平面上,小车AB部分是半径R=0.3m的四分之一光滑圆弧轨道,BC部分是长L=0.25m的水平粗糙轨道,两段轨道相切于B点,水平轨道左端C离地面高度h=0.1m.质量m=lkg的小物块(视为质点)在小车上A点从静止沿轨道下滑,物块与水平轨道间的动摩擦因数μ=0.6,重力加速度取g=10m/s2,求: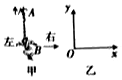 杂技又称“杂伎”,现代杂技特指演员靠自己身体技巧完成一系列高难度动作的表演性节目,如图甲所示,在某次杂技表演中,演员A沿竖直匀速向上爬,同时演员B顶着竖直杆水平匀速向右移动,若建立图乙所示的坐标系,则在这一过程中演员A的运动轨迹可能是下面四幅图中的( )
杂技又称“杂伎”,现代杂技特指演员靠自己身体技巧完成一系列高难度动作的表演性节目,如图甲所示,在某次杂技表演中,演员A沿竖直匀速向上爬,同时演员B顶着竖直杆水平匀速向右移动,若建立图乙所示的坐标系,则在这一过程中演员A的运动轨迹可能是下面四幅图中的( )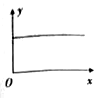

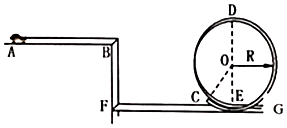 如图所示为一遥控电动赛车(可视为质点)和它运动轨道示意图.假设在某次演示中,赛车从A位置由静止开始运动,经2s后关闭电动机,赛车继续前进至B点后水平飞出,赛车能从C点无碰撞地进入竖直平面内的圆形光滑轨道,D点和E点分别为圆形轨道的最高点和最低点.已知赛车在水平轨道AB段运动时受到的恒定阻力为0.4N,赛车质量
如图所示为一遥控电动赛车(可视为质点)和它运动轨道示意图.假设在某次演示中,赛车从A位置由静止开始运动,经2s后关闭电动机,赛车继续前进至B点后水平飞出,赛车能从C点无碰撞地进入竖直平面内的圆形光滑轨道,D点和E点分别为圆形轨道的最高点和最低点.已知赛车在水平轨道AB段运动时受到的恒定阻力为0.4N,赛车质量