题目内容
7.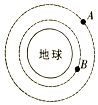 如图所示,两质量相等的卫星A、B绕地球做匀速圆周运动,用R、T、Ek、S分别表示卫星的轨道半径、周期、动能、与地心连线在单位时间内扫过的面积.下列关系式正确的是( )
如图所示,两质量相等的卫星A、B绕地球做匀速圆周运动,用R、T、Ek、S分别表示卫星的轨道半径、周期、动能、与地心连线在单位时间内扫过的面积.下列关系式正确的是( )| A. | TA<TB | B. | EkA>EkB | ||
| C. | SA=SB | D. | $\frac{{R}_{A}^{3}}{{T}_{A}^{2}}$=$\frac{{R}_{B}^{3}}{{T}_{B}^{2}}$ |
分析 根据万有引力提供向心力得出周期、线速度与轨道半径的关系,从而比较周期和线速度的大小,根据开普勒第二定律比较扫过的面积,根据开普勒第三定律得出轨道半径和周期的关系.
解答 解:AD、由开普勒第三定律得:$\frac{{R}_{A}^{3}}{{T}_{A}^{2}}$=$\frac{{R}_{B}^{3}}{{T}_{B}^{2}}$,由图示可知:RA>RB,则:TA>TB,故A错误,D正确;
B、万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,卫星动能:EK=$\frac{1}{2}$mv2=$\frac{GMm}{2r}$,由于卫星质量m相等而RA>RB,则:EKA<EKB,故B错误;
C、由开普勒第二定律可知,绕同一天体运动的天体与中心天体连线在同一时间内扫过的面积相等,即:SA=SB,故C正确;
故选:CD.
点评 本题考查了万有引力定律的应用,解决本题的关键是掌握开普勒第二定律、开普勒第三定律、万有引力公式与牛顿第二定律;应用基础知识即可解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 一辆汽车从静止开始由甲地出发.沿平直公路开往乙地.汽车先做匀加速运动.接着做匀减速运动.开到乙地刚好停止.其速度图象如图所示.那么在0-t0和t0-3t0这两段时间内( )
一辆汽车从静止开始由甲地出发.沿平直公路开往乙地.汽车先做匀加速运动.接着做匀减速运动.开到乙地刚好停止.其速度图象如图所示.那么在0-t0和t0-3t0这两段时间内( )
 一辆汽车从静止开始由甲地出发.沿平直公路开往乙地.汽车先做匀加速运动.接着做匀减速运动.开到乙地刚好停止.其速度图象如图所示.那么在0-t0和t0-3t0这两段时间内( )
一辆汽车从静止开始由甲地出发.沿平直公路开往乙地.汽车先做匀加速运动.接着做匀减速运动.开到乙地刚好停止.其速度图象如图所示.那么在0-t0和t0-3t0这两段时间内( )| A. | 加速度大小之比为2:1 | B. | 加速度大小之比为3;1 | ||
| C. | 加速度大小之比为1:2 | D. | 加速度大小之比为1:3 |
15.下列关于单摆的说法,正确的是( )
| A. | 将同一单摆从山下移到山上,其振动频率减小 | |
| B. | 单摆摆球的回复力是摆球重力沿圆弧切线方向的分力 | |
| C. | 用一装满砂的轻漏斗做成单摆,在开始振动后砂从漏斗中慢慢漏出的过程中,其振动周期逐渐变大 | |
| D. | 单摆在正向最大位移处时的位移为-A(A为振幅) |
2.下列关于物理学史说法正确的是( )
| A. | 爱因斯坦提出了相对性原理光速不变原理 | |
| B. | 牛顿提出了太阳系行星运动三大定律 | |
| C. | 卡文迪许发现了万有引力定律 | |
| D. | 伽利略认为物体的运动需要力来维持 |
12. 如图所示,一个小球从光滑固定斜面顶端由静止滑下,依次经过A、B、C、D四点,已知经过AB、BC和CD三段所用时间分别为t、2t和3t,通过AB段和BC段的位移大小分别为x1和x2,下列说法正确的是( )
如图所示,一个小球从光滑固定斜面顶端由静止滑下,依次经过A、B、C、D四点,已知经过AB、BC和CD三段所用时间分别为t、2t和3t,通过AB段和BC段的位移大小分别为x1和x2,下列说法正确的是( )
 如图所示,一个小球从光滑固定斜面顶端由静止滑下,依次经过A、B、C、D四点,已知经过AB、BC和CD三段所用时间分别为t、2t和3t,通过AB段和BC段的位移大小分别为x1和x2,下列说法正确的是( )
如图所示,一个小球从光滑固定斜面顶端由静止滑下,依次经过A、B、C、D四点,已知经过AB、BC和CD三段所用时间分别为t、2t和3t,通过AB段和BC段的位移大小分别为x1和x2,下列说法正确的是( )| A. | 一定有x2=3x1 | |
| B. | CD段位移大小为4x2-5x1 | |
| C. | 小球的加速度大小为$\frac{{x}_{2}-2{x}_{1}}{3{t}^{2}}$ | |
| D. | 小球在B点的瞬时速度大小为$\frac{4{x}_{1}+{x}_{2}}{6t}$ |
 如图所示,一光滑斜面与水平面平滑相连,水平面的BC部分与滑块(可视为质点)之间的动摩擦因数为μ,水平面的C点与光滑的竖直半圆轨道平滑连接,已知BC=L,轨道半径为R.质量为m的滑块在斜面上的A点由静止释放,滑块恰好经过D点后落在水平面上的E点(未画出).求:
如图所示,一光滑斜面与水平面平滑相连,水平面的BC部分与滑块(可视为质点)之间的动摩擦因数为μ,水平面的C点与光滑的竖直半圆轨道平滑连接,已知BC=L,轨道半径为R.质量为m的滑块在斜面上的A点由静止释放,滑块恰好经过D点后落在水平面上的E点(未画出).求: 如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠B=60°,AB边长为L.一束与BC面成θ=30°角的光从BC面中点射入三棱镜,进入三棱镜后折射光线从AB边平行AC边射出.不考虑光线在AB边上的反射情况.已知光在真空中速度为C.求:
如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠B=60°,AB边长为L.一束与BC面成θ=30°角的光从BC面中点射入三棱镜,进入三棱镜后折射光线从AB边平行AC边射出.不考虑光线在AB边上的反射情况.已知光在真空中速度为C.求: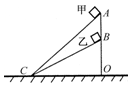 如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )
如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )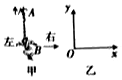 杂技又称“杂伎”,现代杂技特指演员靠自己身体技巧完成一系列高难度动作的表演性节目,如图甲所示,在某次杂技表演中,演员A沿竖直匀速向上爬,同时演员B顶着竖直杆水平匀速向右移动,若建立图乙所示的坐标系,则在这一过程中演员A的运动轨迹可能是下面四幅图中的( )
杂技又称“杂伎”,现代杂技特指演员靠自己身体技巧完成一系列高难度动作的表演性节目,如图甲所示,在某次杂技表演中,演员A沿竖直匀速向上爬,同时演员B顶着竖直杆水平匀速向右移动,若建立图乙所示的坐标系,则在这一过程中演员A的运动轨迹可能是下面四幅图中的( )