题目内容
16.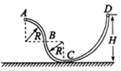 由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )
由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球(小球直径略小于管的直径),从距离水平地面高为H的管口D处静止释放.下列说法正确的是( )| A. | 若小球恰好能够到达水平管口A处,则H>2R | |
| B. | 若小球恰好能够到达水平管口A处,则H=2R | |
| C. | 若小球通过A处时对管壁恰好无压力,则H=$\frac{1}{2}$R | |
| D. | 若小球通过A处时对管壁恰好无压力,则H=$\frac{5}{2}$R |
分析 根据小球在A处的状况,由牛顿第二定律求得速度,然后再根据机械能守恒即可求得H.
解答 解:小球运动过程中只有重力做功,故机械能守恒;
AB、若小球恰好能够到达水平管口A处,那么,小球在A处的速度为零,由机械能守恒可得:D、A等高,即H=2R,故A错误,B正确;
CD、若小球通过A处时对管壁恰好无压力,那么,小球在A处的重力刚好做向心力,即$mg=\frac{m{{v}_{A}}^{2}}{R}$;那么,由机械能守恒可得:$mg(H-2R)=\frac{1}{2}m{{v}_{A}}^{2}=\frac{1}{2}mgR$,所以,$H=\frac{5}{2}R$,故C错误,D正确;
故选:BD.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

练习册系列答案
相关题目
6.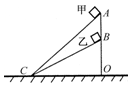 如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )
如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )
 如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )
如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )| A. | Ek1>Ek2 | B. | v1>v2 | ||
| C. | W1<W2 | D. | t1与t2大小关系不确定 |
4.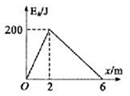 物体在水平桌面上受到水平恒定拉力作用由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )
物体在水平桌面上受到水平恒定拉力作用由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )
 物体在水平桌面上受到水平恒定拉力作用由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )
物体在水平桌面上受到水平恒定拉力作用由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )| A. | 物块的质量 | B. | 物块与桌面之间的滑动摩擦力 | ||
| C. | 水平拉力大小 | D. | 物块在前0~2m内的加速度 |
11.A、B两球在光滑水平面上沿同一直线、同一方向运动,mA=1kg,mB=2kg,vA=6m/s,vB=2m/s,当A球追上B球并发生碰撞后,则A、B两球的速度可能值是( )
| A. | 5m/s、2.5m/s | B. | 2m/s、4m/s | C. | 3m/s、3.5m/s | D. | 7m/s、1.5m/s |
1.悬停在空中的直升飞机上坠落一物体,可视为做自由落体运动.从下落开始计时,重力加速度g取l0m/s2,则物体在第5s内的位移为( )
| A. | 10m | B. | 45m | C. | 80m | D. | 125m |
8. 如图所示,在竖直平面内固定一个半圆形轨道,AB为轨道的水平直径,O为圆心.现从A点分别以速度v1、v2沿水平方向抛出甲、乙两个相同的小球并分别落在M、N两点已知OM、ON与竖直方向的夹角均为30°,不考虑空气阻力,则下列结论正确的是( )
如图所示,在竖直平面内固定一个半圆形轨道,AB为轨道的水平直径,O为圆心.现从A点分别以速度v1、v2沿水平方向抛出甲、乙两个相同的小球并分别落在M、N两点已知OM、ON与竖直方向的夹角均为30°,不考虑空气阻力,则下列结论正确的是( )
 如图所示,在竖直平面内固定一个半圆形轨道,AB为轨道的水平直径,O为圆心.现从A点分别以速度v1、v2沿水平方向抛出甲、乙两个相同的小球并分别落在M、N两点已知OM、ON与竖直方向的夹角均为30°,不考虑空气阻力,则下列结论正确的是( )
如图所示,在竖直平面内固定一个半圆形轨道,AB为轨道的水平直径,O为圆心.现从A点分别以速度v1、v2沿水平方向抛出甲、乙两个相同的小球并分别落在M、N两点已知OM、ON与竖直方向的夹角均为30°,不考虑空气阻力,则下列结论正确的是( )| A. | 甲球比乙球先落到轨道上 | |
| B. | 甲、乙两球在下落过程中受到的冲量相同 | |
| C. | v1:v2=1:2 | |
| D. | v1:v2=1:3 |
6. 质量为m的物体,在汽车的牵引下由静止开始运动,当物体上升h高度时,汽车的速度为v,细绳与水平面间的夹角为θ,则下列说法中正确的是( )
质量为m的物体,在汽车的牵引下由静止开始运动,当物体上升h高度时,汽车的速度为v,细绳与水平面间的夹角为θ,则下列说法中正确的是( )
 质量为m的物体,在汽车的牵引下由静止开始运动,当物体上升h高度时,汽车的速度为v,细绳与水平面间的夹角为θ,则下列说法中正确的是( )
质量为m的物体,在汽车的牵引下由静止开始运动,当物体上升h高度时,汽车的速度为v,细绳与水平面间的夹角为θ,则下列说法中正确的是( )| A. | 此时物体的速度大小为vsinθ | |
| B. | 此时物体的速度大小为v•cosθ | |
| C. | 汽车对物体做的功为mgh | |
| D. | 汽车对物体做的功为mgh+$\frac{{m(vsinθ)}^{2}}{2}$ |
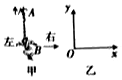 杂技又称“杂伎”,现代杂技特指演员靠自己身体技巧完成一系列高难度动作的表演性节目,如图甲所示,在某次杂技表演中,演员A沿竖直匀速向上爬,同时演员B顶着竖直杆水平匀速向右移动,若建立图乙所示的坐标系,则在这一过程中演员A的运动轨迹可能是下面四幅图中的( )
杂技又称“杂伎”,现代杂技特指演员靠自己身体技巧完成一系列高难度动作的表演性节目,如图甲所示,在某次杂技表演中,演员A沿竖直匀速向上爬,同时演员B顶着竖直杆水平匀速向右移动,若建立图乙所示的坐标系,则在这一过程中演员A的运动轨迹可能是下面四幅图中的( )

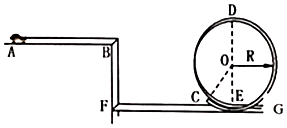 如图所示为一遥控电动赛车(可视为质点)和它运动轨道示意图.假设在某次演示中,赛车从A位置由静止开始运动,经2s后关闭电动机,赛车继续前进至B点后水平飞出,赛车能从C点无碰撞地进入竖直平面内的圆形光滑轨道,D点和E点分别为圆形轨道的最高点和最低点.已知赛车在水平轨道AB段运动时受到的恒定阻力为0.4N,赛车质量
如图所示为一遥控电动赛车(可视为质点)和它运动轨道示意图.假设在某次演示中,赛车从A位置由静止开始运动,经2s后关闭电动机,赛车继续前进至B点后水平飞出,赛车能从C点无碰撞地进入竖直平面内的圆形光滑轨道,D点和E点分别为圆形轨道的最高点和最低点.已知赛车在水平轨道AB段运动时受到的恒定阻力为0.4N,赛车质量