题目内容
1.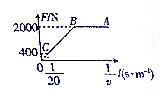 在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )
在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )| A. | 在AB过程中,电动车做匀加速运动 | |
| B. | 在整个过程中,电动车受到的阻力为2000N | |
| C. | 在整个过程中,电动车发动机的最大功率为8000W | |
| D. | 在整个过程中,电动车克服阻力做的功为72000J |
分析 AB过程牵引力不变,根据牛顿第二定律知,做匀加速直线运动,BC段图线的斜率表示电动车的功率,斜率不变,则功率不变,根据功率与牵引力的关系,判断BC段的运动情况,速度达到最大时,牵引力等于阻力.
解答 解:A、AB过程牵引力不变,受到的阻力也不变,根据牛顿第二定律知,做匀加速直线运动.故A正确;
B、由图可知,当最大速度vmax=20m/s时,牵引力为Fmin=400N,故恒定阻力 f=Fmin=400N,此时为C点,故B错误;
C、根据瞬时功率的公式可知,额定功率为:P=Fminvmax=400×20=8000W.故C正确;
D、匀加速运动的末速度为:$v=\frac{P}{F}$
代入数据解得:v=4m/s
匀加速运动的加速度为:$a=\frac{F-f}{m}$
代入数据解得:a=2m/s2
电动车在速度达到4m/s之前,一直做匀加速直线运动,故所求时间为:$t=\frac{v}{a}$=$\frac{4}{2}=2$s
匀加速通过的位移为:x=$\frac{1}{2}a{t}^{2}=\frac{1}{2}×2×{2}^{2}=4$m
额定功率作用下由动能定理有:$P({t}_{总}-t)-fx′=\frac{1}{2}{mv}_{max}^{2}-\frac{1}{2}m{v}^{2}$
解得:x′=35.2m
故总位移为:x总=x+x′=4m+35.2m=39.2m
电动车克服阻力做的功为:W=fx=400×39.2=15680J,故D错误
故选:AC
点评 解决本题的关键能够从图线中分析出电动车在整个过程中的运动情况,当牵引力等于阻力时,速度达到最大.

练习册系列答案
相关题目
2.下列关于物理学史说法正确的是( )
| A. | 爱因斯坦提出了相对性原理光速不变原理 | |
| B. | 牛顿提出了太阳系行星运动三大定律 | |
| C. | 卡文迪许发现了万有引力定律 | |
| D. | 伽利略认为物体的运动需要力来维持 |
6.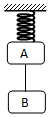 如图,轻质弹簧下挂重为300N的物体A时伸长了3cm,再挂上重为200N的物体B时又伸长了2cm,现将AB间的细线烧断,使A在竖直平面内振动,则( )
如图,轻质弹簧下挂重为300N的物体A时伸长了3cm,再挂上重为200N的物体B时又伸长了2cm,现将AB间的细线烧断,使A在竖直平面内振动,则( )
 如图,轻质弹簧下挂重为300N的物体A时伸长了3cm,再挂上重为200N的物体B时又伸长了2cm,现将AB间的细线烧断,使A在竖直平面内振动,则( )
如图,轻质弹簧下挂重为300N的物体A时伸长了3cm,再挂上重为200N的物体B时又伸长了2cm,现将AB间的细线烧断,使A在竖直平面内振动,则( )| A. | 最大回复力为300N,振幅为2cm | |
| B. | 最大回复力为200N,振幅为3cm | |
| C. | 只减小A的质量,振动的振幅变小,周期不变 | |
| D. | 只减小B的质量,振动的振幅变小,周期不变 |
6.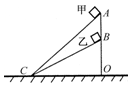 如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )
如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )
 如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )
如图所示,AC和BC是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别为m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C 时的动能分别为Ek1、Ek2,速度大小分别为v1、v2.甲、乙在下滑至底端C的过程中克服摩擦力做的功分别为W1、W2,所需时间分别为t1、t2.则( )| A. | Ek1>Ek2 | B. | v1>v2 | ||
| C. | W1<W2 | D. | t1与t2大小关系不确定 |
10.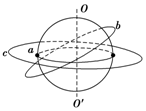 如图所示,a为赤道上的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球的同步卫星,已知地球半径为R,地球同步卫星轨道半径为6.6R;下列说法中正确的是( )
如图所示,a为赤道上的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球的同步卫星,已知地球半径为R,地球同步卫星轨道半径为6.6R;下列说法中正确的是( )
 如图所示,a为赤道上的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球的同步卫星,已知地球半径为R,地球同步卫星轨道半径为6.6R;下列说法中正确的是( )
如图所示,a为赤道上的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球的同步卫星,已知地球半径为R,地球同步卫星轨道半径为6.6R;下列说法中正确的是( )| A. | a和c的向心加速度之比为1:6.6 | B. | b和c的向心加速度之比为6.6:1 | ||
| C. | a的运转周期大于c的运转周期 | D. | b的运转周期大于c的运转周期 |
11.A、B两球在光滑水平面上沿同一直线、同一方向运动,mA=1kg,mB=2kg,vA=6m/s,vB=2m/s,当A球追上B球并发生碰撞后,则A、B两球的速度可能值是( )
| A. | 5m/s、2.5m/s | B. | 2m/s、4m/s | C. | 3m/s、3.5m/s | D. | 7m/s、1.5m/s |
 一个质量为0.3kg的物体沿水平面做直线运动,如图所示,图线a表示物体受水平拉力时的 v-t 图象,图线b表示撤去水平拉力后物体继续运动的 v-t 图象,g=10m/s2,求:
一个质量为0.3kg的物体沿水平面做直线运动,如图所示,图线a表示物体受水平拉力时的 v-t 图象,图线b表示撤去水平拉力后物体继续运动的 v-t 图象,g=10m/s2,求: 如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠B=60°,AB边长为L.一束与BC面成θ=30°角的光从BC面中点射入三棱镜,进入三棱镜后折射光线从AB边平行AC边射出.不考虑光线在AB边上的反射情况.已知光在真空中速度为C.求:
如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠B=60°,AB边长为L.一束与BC面成θ=30°角的光从BC面中点射入三棱镜,进入三棱镜后折射光线从AB边平行AC边射出.不考虑光线在AB边上的反射情况.已知光在真空中速度为C.求: