题目内容
18.2013年12月2日1时30分,我国成功发射了“嫦娥三号”探月卫星,12月6日17时47分顺利进入环月轨道.若该卫星在地球表面的重力为G1,在月球表面的重力为G2,已知地球半径为R1,月球半径为R2,地球表面处的重力加速度为g,则( )| A. | 月球表面处的重力加速度g月为 $\frac{G_2}{G_1}g$ | |
| B. | 月球的质量与地球的质量之比为$\frac{{{G_1}R_2^2}}{{{G_2}R_1^2}}$ | |
| C. | 卫星在距月球表面轨道上做匀速圆周运动的周期T月为2π$\sqrt{\frac{{{R_2}{G_1}}}{{g{G_2}}}}$ | |
| D. | 月球的第一宇宙速度与地球的第一宇宙速度之比为$\sqrt{\frac{{{G_1}{R_2}}}{{{G_2}{R_1}}}}$ |
分析 卫星在地球表面的重力为G1,地球表面处的重力加速度为g,由G1=mg,求出卫星的质量,再G2=mg月求出g月.根据g=$\frac{GM}{{R}^{2}}$,由两星球的半径和表面重力加速度分别求出地球和月球的质量.卫星在距月球表面轨道上做匀速圆周运动时,由月球的万有引力提供向心力,根据牛顿第二定律求出卫星的周期.地球的第一宇宙速度为v地=$\sqrt{g{R}_{1}}$,月球的第一宇宙速度为v月=$\sqrt{{g}_{月}{R}_{2}}$,将G1=mg,G2=mg月代入求出第一宇宙速度之比.
解答 解:A、卫星的质量为m=$\frac{{G}_{1}}{g}$,月球表面处的重力加速度g月=$\frac{{G}_{2}}{m}$=$\frac{{G}_{2}}{{G}_{1}}$g.故A正确;
B、由g=$\frac{GM}{{R}^{2}}$,得到月球的质量M月=$\frac{{g}_{月}{{R}_{2}}^{2}}{G}$,M地=$\frac{g{{R}_{1}}^{2}}{G}$,又$\frac{{g}_{月}}{g}=\frac{{G}_{2}}{{G}_{1}}$,整理得,月球的质量与地球的质量之比为$\frac{{G}_{2}{{R}_{2}}^{2}}{{G}_{1}{{R}_{1}}^{2}}$.故B错误;
C、设卫星质量为m,由mg月=m$\frac{4{π}^{2}}{{T}^{2}}{R}_{月}$,g月=$\frac{{G}_{2}}{{G}_{1}}g$,解得T月=2π$\sqrt{\frac{{R}_{2}{G}_{1}}{g{G}_{2}}}$.故C正确;
D、月球的第一宇宙速度为v月=$\sqrt{{g}_{月}{R}_{2}}$,地球的第一宇宙速度为v地=$\sqrt{g{R}_{1}}$,将G1=mg,G2=mg月代入解得:$\frac{{v}_{月}}{{v}_{地}}=\sqrt{\frac{{G}_{2}{R}_{2}}{{G}_{1}{R}_{1}}}$.故D错误.
故选:AC.
点评 本题是卫星类型的问题,关键是构建物理模型,再运用数学变换进行分析处理.

 如图所示,在两个固定的异种点电荷Q1、Q2的连线上有A、B两点.将一个带负电的试探电荷q由A静止释放,它从A点运动到B点的过程中,可能( )
如图所示,在两个固定的异种点电荷Q1、Q2的连线上有A、B两点.将一个带负电的试探电荷q由A静止释放,它从A点运动到B点的过程中,可能( )| A. | 先加速运动再减速运动 | B. | 加速度一直增大 | ||
| C. | 电势能先增大后减小 | D. | 在B点电势能比在A点的电势能大 |

| A. | 木块所受的合外力为零 | |
| B. | 木块所受的力都不对其做功 | |
| C. | 木块的机械能守恒 | |
| D. | 木块所受的合外力不为零,但合外力对木块所做的功为零 |
 如图所示,在第一象限存在匀强电场,场强沿y轴负方向;在第二象限有两块平行金属板M、N组成的加速电场,板间的电压为U.一电荷量为+q、质量为m的带电粒子,靠近M板由静止释放,经N板小孔沿x轴正方向飞出,经过y轴上y=h处的点P1进入匀强电场,然后,在经过x轴上P2点进入第四象限时其速度与x轴正方向的夹角θ=53°,不计粒子的重力,已知sin53°=0.8,cos53°=0.6,求:
如图所示,在第一象限存在匀强电场,场强沿y轴负方向;在第二象限有两块平行金属板M、N组成的加速电场,板间的电压为U.一电荷量为+q、质量为m的带电粒子,靠近M板由静止释放,经N板小孔沿x轴正方向飞出,经过y轴上y=h处的点P1进入匀强电场,然后,在经过x轴上P2点进入第四象限时其速度与x轴正方向的夹角θ=53°,不计粒子的重力,已知sin53°=0.8,cos53°=0.6,求: 如图所示,质量M=8kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=8N,当小车向右运动的速度达到1.5m/s时,在小车前端轻轻地放上一个大小不计,质量为m=2kg的小物块,物块与小车间的动摩擦因数 μ=0.2,小车足够长(取g=10m/s2).求:
如图所示,质量M=8kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=8N,当小车向右运动的速度达到1.5m/s时,在小车前端轻轻地放上一个大小不计,质量为m=2kg的小物块,物块与小车间的动摩擦因数 μ=0.2,小车足够长(取g=10m/s2).求: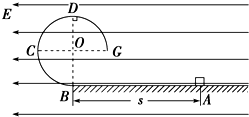 如图所示,BCDG是光滑绝缘的$\frac{3}{4}$圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为$\frac{3}{4}$mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.
如图所示,BCDG是光滑绝缘的$\frac{3}{4}$圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为$\frac{3}{4}$mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.