题目内容
12.如图所示,图甲是某人设计的一种振动发电装置,它的结构是一个半径为r=0.1m的有25匝的线圈套在辐向形永久磁铁槽中,磁场的磁感线均沿半径方向均匀分布(其右视图如图乙所示).在线圈所在位置磁感应强度B的大小均为$\frac{1}{π}$T,线圈的电阻为2Ω,它的引出线接有8Ω的电珠L,外力推动线圈的P端,做往复运动,便有电流通过电珠.当线圈向右的位移随时间t变化的规律如图丙所示时(x取向右为正):(1)试画出感应电流随时间变化的图象(取图乙中逆时针电流为正);
(2)求每一次推动线圈运动过程中的作用力:
(3)求该发动机的输出功率(摩擦等损耗不计).

分析 (1)由图丙求出线圈运动的速度,由E=BLv求出感应电动势,然后由欧姆定律求出感应电流,由此画图;
(2)由F=BIL求出安培力,由平衡条件求出推力大小.
(3)小灯泡是外电路,小电珠的功率是发电机的输出功率,由P=I2R求出输出功率.
解答 解:(1)从图丙可以看出,线圈往返的每次运动都是匀速直线运动,其速度为v=$\frac{△x}{△t}=\frac{0.08}{0.1}$m/s=0.8 m/s
线圈左右运动时做切割磁感线运动产生的感应电动势为:E=2nπrBv=2×25×π×0.1×$\frac{1}{π}$×0.8 V=4.0 V
根据闭合电路的欧姆定律可得感应电流 I=$\frac{E}{{R}_{1}+{R}_{2}}=\frac{4}{2+8}$A=0.40A
电流图象如图所示.
(2)由于线圈每次运动都是匀速直线运动,所以每次运动过程中推力必须等于安培力.
F推=F安=nBIL=2nBIπr=2×25×$\frac{1}{π}$×0.4×π×0.1 N=2 N.
(3)发电机的输出功率即灯的电功率.P=I2R2=0.42×8 W=1.28 W.
答:(1)感应电流随时间变化的图象见解析;
(2)每一次推动线圈运动过程中的作用力为2N:
(3)该发动机的输出功率为1.28 W.
点评 本题主要是考查了法拉第电磁感应定律和闭合电路的欧姆定律;对于导体切割磁感应线产生的感应电动势的计算公式E=BLv,要知道L为有效切割长度.

练习册系列答案
相关题目
18. 甲、乙两车在同一条直道上行驶,它们运动的位移s随时间t变化的关系如图所示,已知乙车做匀变速直线运动,其图线与t轴相切于10s处,则下列说法中正确的是( )
甲、乙两车在同一条直道上行驶,它们运动的位移s随时间t变化的关系如图所示,已知乙车做匀变速直线运动,其图线与t轴相切于10s处,则下列说法中正确的是( )
 甲、乙两车在同一条直道上行驶,它们运动的位移s随时间t变化的关系如图所示,已知乙车做匀变速直线运动,其图线与t轴相切于10s处,则下列说法中正确的是( )
甲、乙两车在同一条直道上行驶,它们运动的位移s随时间t变化的关系如图所示,已知乙车做匀变速直线运动,其图线与t轴相切于10s处,则下列说法中正确的是( )| A. | 乙车的加速度大小为1.6m/s2 | B. | 乙车的初位置在s0=60m处 | ||
| C. | 甲车的初速度为零 | D. | 5s时两车相遇,此时甲车速度较大 |
7.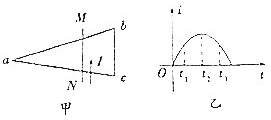 等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )
等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )
 等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )
等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )| A. | 在任何时刻线框中都无感应电流 | |
| B. | 在t1时刻线框中有沿acba方向的感应电流 | |
| C. | 在t2时刻线框中有沿acba方向的感应电流 | |
| D. | 在t3时刻线框中有沿abca方向的感应电流 |
17. 质量为m的小球在竖直向上的拉力作用下从静止开始运动,其v-t图象如图所示(竖直向上为正方向,DE段为直线),已知重力加速度大小为g,下列说法正确的是( )
质量为m的小球在竖直向上的拉力作用下从静止开始运动,其v-t图象如图所示(竖直向上为正方向,DE段为直线),已知重力加速度大小为g,下列说法正确的是( )
 质量为m的小球在竖直向上的拉力作用下从静止开始运动,其v-t图象如图所示(竖直向上为正方向,DE段为直线),已知重力加速度大小为g,下列说法正确的是( )
质量为m的小球在竖直向上的拉力作用下从静止开始运动,其v-t图象如图所示(竖直向上为正方向,DE段为直线),已知重力加速度大小为g,下列说法正确的是( )| A. | t3-t4时间内,小球竖直向下做匀减速直线运动 | |
| B. | t0-t2时间内,合力对小球先做正功后做负功 | |
| C. | 0-t2时间内,小球的平均速度一定为$\frac{{v}_{3}}{2}$ | |
| D. | t3-t4时间内,拉力做的功为$\frac{m({v}_{3}+{v}_{4})}{2}$[(v4-v3)+g(t4-t3)] |
4.质量是15kg的小汽车在水平路面上滑行18m后速度从10m/s减小到8m/s,则小车所受的阻力为( )
| A. | 10N | B. | 15N | C. | 20N | D. | 25N |
 如图所示,a、b、c、d分别是四根半径都为R、表面光滑的圆柱体的横截面,彼此靠得很近,形成四个宽度极窄的狭缝1、2、3、4;在这些狭缝和四个圆柱所包围的空间内存在匀强磁场,磁场方向垂直于纸面指向纸里,整个空间为真空.质量为m、电荷量为q的带正电的粒子,从A点由静止经电压为U的电场加速后,沿与a、b都相切的方向由缝1射入磁场,恰好能从缝2沿与b、c都相切的方向射出.设粒子与圆柱表面只发生一次碰撞,碰撞后粒子的速度大小不变,方向相反,碰撞时间极短,且碰撞不改变粒子的电荷量,不计粒子的重力.求:
如图所示,a、b、c、d分别是四根半径都为R、表面光滑的圆柱体的横截面,彼此靠得很近,形成四个宽度极窄的狭缝1、2、3、4;在这些狭缝和四个圆柱所包围的空间内存在匀强磁场,磁场方向垂直于纸面指向纸里,整个空间为真空.质量为m、电荷量为q的带正电的粒子,从A点由静止经电压为U的电场加速后,沿与a、b都相切的方向由缝1射入磁场,恰好能从缝2沿与b、c都相切的方向射出.设粒子与圆柱表面只发生一次碰撞,碰撞后粒子的速度大小不变,方向相反,碰撞时间极短,且碰撞不改变粒子的电荷量,不计粒子的重力.求: 如图,光滑的竖直导轨放置于匀强磁场B中,宽为L,放有一根导体棒ab,其接入导轨电阻为r,由静止开始运动,外电阻为R,分析ab的受力情况和运动情况,并求出ab的最大速度.
如图,光滑的竖直导轨放置于匀强磁场B中,宽为L,放有一根导体棒ab,其接入导轨电阻为r,由静止开始运动,外电阻为R,分析ab的受力情况和运动情况,并求出ab的最大速度. 如图所示的图象表示的是位移-时间图象.AB段表示物体处于静止状态.BC段表示物体做匀速直线运动,其运动方向与选定的正方向相同.CD段表示物体做匀速直线运动,其运动方向与选定的正方向相反.
如图所示的图象表示的是位移-时间图象.AB段表示物体处于静止状态.BC段表示物体做匀速直线运动,其运动方向与选定的正方向相同.CD段表示物体做匀速直线运动,其运动方向与选定的正方向相反. 如图1所示,在“利用自由落体运动验证机械能守恒定律”的实验中,让重锤拖着穿过打点计时器的纸带做自由落体运动,测量重锤的重力势能减少量和动能增加量,从而验证机械能守恒定律.
如图1所示,在“利用自由落体运动验证机械能守恒定律”的实验中,让重锤拖着穿过打点计时器的纸带做自由落体运动,测量重锤的重力势能减少量和动能增加量,从而验证机械能守恒定律.