题目内容
1. 一位同学利用光电加速器等器材做实验来验证自由落体运动是匀变速直线运动,如图甲所示,该同学让一直径为d、质量为m的金属小球从O处由静止释放,下落过程中能通过O处正下方,固定于M处的光电门,测得O、M间的距离为H(H>>d),光电计时器记录下小球通过光电门的时间为t,当地的重力加速度为g.
一位同学利用光电加速器等器材做实验来验证自由落体运动是匀变速直线运动,如图甲所示,该同学让一直径为d、质量为m的金属小球从O处由静止释放,下落过程中能通过O处正下方,固定于M处的光电门,测得O、M间的距离为H(H>>d),光电计时器记录下小球通过光电门的时间为t,当地的重力加速度为g.(1)该同学用游标卡尺测量小球的直径,所测结果如图乙所示,则小球的直径d=10.20mm.
(2)为了用图象法处理实验数据,该同学通过多次改变高度H,重复上述实验,然后以H为横轴,以$\frac{1}{{t}^{2}}$为纵轴,作出了$\frac{1}{{t}^{2}}$-H图象是一条直线,说明自由落体运动是匀变速直线运动.若直线的斜率为k,则加速度的表达式为g=$\frac{k{d}^{2}}{2}$.
分析 (1)游标卡尺读数为固定刻度读数+游标刻度读数,没有估计值;
(2)根据某段时间内的平均速度等于中时刻的瞬时速度,根据mgh=$\frac{1}{2}$mv2,得到$\frac{1}{{t}^{2}}$-H的关系式,分析$\frac{1}{{t}^{2}}$-H图象斜率的物理意义.
解答 解:(1)游标卡尺读数为d=10mm+4×0.05mm=10.20mm,
(2)由某段时间内的平均速度等于中时刻的瞬时速度得,小球经过光电门时的瞬时速度v=$\frac{d}{t}$;
由mgH=$\frac{1}{2}$mv2,得$\frac{1}{{t}^{2}}=\frac{2g}{{d}^{2}}H$,则$\frac{1}{{t}^{2}}$-H图象的斜率k=$\frac{2g}{{d}^{2}}$,故g=$\frac{k{d}^{2}}{2}$.
故答案为:(1)①10.20;②$\frac{k{d}^{2}}{2}$
点评 本实验以小球做自由落体运动为例,验证机械能守恒定律,根据方程mgh=$\frac{1}{2}$mv2,分析$\frac{{v}^{2}}{2}$-h图象斜率的意义是常用的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.据报道在太阳系之外发现了一颗可能适合人类居住的类地行星Gliese581C,天文学观察发现绕该行星做圆周运动的卫星的轨道半径为月球绕地球做圆周运动半径的p倍,周期为月球绕地球做圆周运动周期的q倍.已知地球半径为R,表面重力加速度为g.万有引力常量为G,则该行星的质量为( )
| A. | $\frac{gR{p}^{2}}{G{p}^{3}}$ | B. | $\frac{g{R}^{2}{q}^{3}}{G{p}^{2}}$ | C. | $\frac{gR{q}^{2}}{G{p}^{3}}$ | D. | $\frac{g{R}^{2}{p}^{3}}{G{q}^{2}}$ |
16.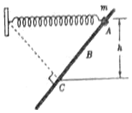 如图所示,轻弹簧一端固定,另一端与质量为m、套在倾斜固定杆A处的圆环相连,弹簧水平.圆环从A处由静止释放,经过杆上B处的速度最大,到达C处的速度为零,在C处时弹簧处于原长且弹簧与斜杆垂直,A、C高度差为h.如果圆环在C处获得一沿斜杆向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
如图所示,轻弹簧一端固定,另一端与质量为m、套在倾斜固定杆A处的圆环相连,弹簧水平.圆环从A处由静止释放,经过杆上B处的速度最大,到达C处的速度为零,在C处时弹簧处于原长且弹簧与斜杆垂直,A、C高度差为h.如果圆环在C处获得一沿斜杆向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
 如图所示,轻弹簧一端固定,另一端与质量为m、套在倾斜固定杆A处的圆环相连,弹簧水平.圆环从A处由静止释放,经过杆上B处的速度最大,到达C处的速度为零,在C处时弹簧处于原长且弹簧与斜杆垂直,A、C高度差为h.如果圆环在C处获得一沿斜杆向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
如图所示,轻弹簧一端固定,另一端与质量为m、套在倾斜固定杆A处的圆环相连,弹簧水平.圆环从A处由静止释放,经过杆上B处的速度最大,到达C处的速度为零,在C处时弹簧处于原长且弹簧与斜杆垂直,A、C高度差为h.如果圆环在C处获得一沿斜杆向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )| A. | 下滑过程中,加速度一直减小 | |
| B. | 上滑经过B的速度大于下滑经过B的速度 | |
| C. | 下滑过程中,克服摩擦力做的功为$\frac{1}{4}$mv2 | |
| D. | 在A处,弹簧的弹性势能为mgh-$\frac{1}{4}$mv2 |
6.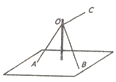 如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
 如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )| A. | 20$\sqrt{3}$N | B. | 40N | C. | 40$\sqrt{3}$N | D. | 60N |
15.下列各组物理量中,全部是矢量的是( )
| A. | 位移、时间、速度、加速度 | B. | 质量、路程、速率、速度 | ||
| C. | 平均速度、位移、加速度、力 | D. | 位移、路程、加速度、速率 |
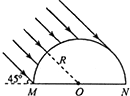 将长为l的玻璃圆柱体沿轴剖开后得到一块半圆柱体,其截面的正视图如图所示,MNPQ为其底面(PQ图中未画出),MN为直径.已知半圆的圆心为O、半径为R,玻璃的折射率n=$\sqrt{2}$.一束与MNPQ所在平面成45°且垂直于轴的平行光束射到半圆柱面上,经折射后,有部分光能从MNPQ面射出,忽略经多次反射到达MNPQ面的光线,求MNPQ透光部分的面积.
将长为l的玻璃圆柱体沿轴剖开后得到一块半圆柱体,其截面的正视图如图所示,MNPQ为其底面(PQ图中未画出),MN为直径.已知半圆的圆心为O、半径为R,玻璃的折射率n=$\sqrt{2}$.一束与MNPQ所在平面成45°且垂直于轴的平行光束射到半圆柱面上,经折射后,有部分光能从MNPQ面射出,忽略经多次反射到达MNPQ面的光线,求MNPQ透光部分的面积.
 如图所示,用力F把铁块压在竖直墙上,此时重力为G的物体沿墙壁匀速下滑,若物体与墙壁之间的动摩擦因数为μ,则物体所受摩擦力的大小等于μF或等于G.
如图所示,用力F把铁块压在竖直墙上,此时重力为G的物体沿墙壁匀速下滑,若物体与墙壁之间的动摩擦因数为μ,则物体所受摩擦力的大小等于μF或等于G.